| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 6 Triangles
This solutions guide delves into Chapter 6: Triangles, shifting the focus from the concept of congruence (identical shape and size) to the equally important but distinct concept of similarity. While congruence deals with exact replicas, similarity addresses figures that maintain the same shape but may differ in size. This chapter explores the conditions under which triangles are deemed similar, investigates the profound theorems arising from these conditions, and revisits the fundamental Pythagoras theorem, now proving it rigorously using the principles of similarity. Understanding similarity is crucial for scaling geometric figures, analyzing proportions, and solving a wide range of problems in geometry and its applications, such as map-making, engineering design, and perspective drawing.
The journey begins with a precise definition of similar figures and, more specifically, similar triangles. Two triangles are similar if, and only if, two conditions are met simultaneously:
- Their corresponding angles are equal. (e.g., if $\triangle ABC \sim \triangle PQR$, then $\angle A = \angle P$, $\angle B = \angle Q$, $\angle C = \angle R$).
- Their corresponding sides are in the same ratio, meaning they are proportional. (e.g., $\frac{AB}{PQ} = \frac{BC}{QR} = \frac{CA}{RP} = k$, where $k$ is the scale factor).
Establishing similarity doesn't always require checking all angles and all sides. Like congruence criteria, there are specific minimal conditions, known as similarity criteria, that guarantee two triangles are similar. The solutions explain and extensively apply these criteria:
- AA (Angle-Angle) Similarity: If two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar. (The third angles must also be equal due to the angle sum property).
- SAS (Side-Angle-Side) Similarity: If one angle of a triangle is equal to one angle of another triangle and the sides including these angles are proportional, then the triangles are similar.
- SSS (Side-Side-Side) Similarity: If the corresponding sides of two triangles are proportional, then their corresponding angles are equal, and the triangles are similar.
Solutions demonstrate using these criteria to formally prove triangle similarity ($\triangle ABC \sim \triangle PQR$) and subsequently leveraging the properties of similar triangles (equal angles or proportional sides) to deduce unknown lengths or angles.
Two pivotal theorems concerning proportionality within triangles are thoroughly explored:
The Basic Proportionality Theorem (BPT), also known as Thales Theorem, is a cornerstone result. It states that if a line is drawn parallel to one side of a triangle intersecting the other two sides at distinct points, then the line divides the other two sides in the same ratio. Solutions provide detailed proofs and numerous examples showcasing its application in finding segment lengths.
The Converse of BPT is equally important: If a line divides any two sides of a triangle in the same ratio, then the line must be parallel to the third side. Solutions illustrate how this converse is used to prove lines are parallel based on segment ratios.
Furthermore, the relationship between the areas of similar triangles is established through a key theorem: The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. This principle extends to other corresponding linear elements like altitudes, medians, and angle bisectors. For instance, if $\triangle ABC \sim \triangle PQR$, then $\frac{Area(\triangle ABC)}{Area(\triangle PQR)} = (\frac{AB}{PQ})^2 = (\frac{BC}{QR})^2 = (\frac{CA}{RP})^2$. Solutions demonstrate the proof and application of this area relationship.
Finally, the chapter provides rigorous proofs for the Pythagoras Theorem (in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides, $a^2 + b^2 = c^2$) and its Converse, utilizing the concepts of triangle similarity developed earlier. This offers a deeper understanding compared to previous introductions. Extensive practice problems involving right-angled triangles are solved using these theorems. Throughout this chapter's solutions, the emphasis remains firmly on constructing logical proofs and accurately applying the criteria and theorems of similarity.
Exercise 6.1
Question 1. Fill in the blanks using the correct word given in brackets :
(i) All circles are ______________ (congruent, similar)
(ii) All squares are ____________. (similar, congruent)
(iii) All _______________triangles are similar. (isosceles, equilateral)
(iv) Two polygons of the same number of sides are similar, if (a) their corresponding angles are _____________________and (b) their corresponding sides are .(equal,)
Answer:
Let's fill in the blanks based on the definitions of similar figures.
(i) All circles are similar (congruent, similar)
Circles are similar because they have the same shape, regardless of their size. Congruent circles must have the same radius.
(ii) All squares are similar. (similar, congruent)
Squares are similar because all squares have four equal sides and four right angles ($90^\circ$). Their shape is determined, only the size can vary. Congruent squares must have the same side length.
(iii) All equilateral triangles are similar. (isosceles, equilateral)
Equilateral triangles are similar because all equilateral triangles have three equal sides and three equal angles ($60^\circ$). Isosceles triangles only have two equal sides and two equal angles, and their shape can vary (e.g., a right isosceles triangle is not similar to an acute isosceles triangle).
(iv) Two polygons of the same number of sides are similar, if (a) their corresponding angles are equal and (b) their corresponding sides are proportional.
These are the two conditions for similarity of polygons. Corresponding angles must be equal, and the ratio of corresponding sides must be constant (proportional).
Question 2. Give two different examples of pair of
(i) similar figures.
(ii) non-similar figures.
Answer:
Let's provide examples based on the definition of similar figures (same shape, possibly different size) and non-similar figures (different shapes).
(i) Similar figures:
Two figures are similar if they have the same shape but not necessarily the same size. The ratio of corresponding sides is proportional, and corresponding angles are equal.
Example 1: Two circles of different radii. Circles of any size are always round, so they have the same shape. For example, a circle with radius 2 cm and a circle with radius 5 cm are similar.
Example 2: Two squares of different side lengths. All squares have four equal sides and four right angles ($90^\circ$). Their shape is fixed. For example, a square with side length 3 cm and a square with side length 7 cm are similar.
(Other examples include: two equilateral triangles, two photographs of the same scene enlarged or reduced, a map and the actual geographic area it represents).
(ii) Non-similar figures:
Two figures are non-similar if they do not have the same shape.
Example 1: A circle and a square. A circle is round and a square has straight sides and corners. They clearly do not have the same shape.
Example 2: A triangle and a rectangle. A triangle has three sides and three angles, while a rectangle has four sides and four angles. They do not have the same shape.
(Other examples include: a right-angled triangle and an equilateral triangle, a square and a rectangle that is not a square, a circle and a line segment).
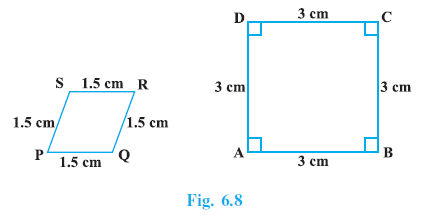
Question 3. State whether the following quadrilaterals are similar or not:
Answer:
Two polygons of the same number of sides are similar if:
(a) Their corresponding angles are equal.
(b) Their corresponding sides are in the same ratio (proportional).
Let's examine the two quadrilaterals shown in the figure: a square PQRS and a rhombus ABCD.
Check the corresponding angles:
In the square PQRS, all angles are right angles ($90^\circ$). So, $\angle P = \angle Q = \angle R = \angle S = 90^\circ$.
In the rhombus ABCD, the angles are not all $90^\circ$. From the figure, $\angle A \neq 90^\circ$, $\angle B \neq 90^\circ$, $\angle C \neq 90^\circ$, $\angle D \neq 90^\circ$.
For similarity, corresponding angles must be equal. Since the angles of the square are $90^\circ$ and the angles of the rhombus are not all $90^\circ$, the corresponding angles are not equal.
Check the ratio of corresponding sides:
In the square PQRS, all sides are equal. Let's say PQ = QR = RS = SP = 3 cm (from the scale indicated in the figure).
In the rhombus ABCD, all sides are equal. Let's say AB = BC = CD = DA = 3 cm (from the scale indicated in the figure).
So, the ratio of corresponding sides (e.g., AB to PQ, BC to QR, etc.) is $\frac{3 \text{ cm}}{3 \text{ cm}} = 1$. The corresponding sides are proportional (in fact, they are equal in length in this specific figure). The ratio of corresponding sides is constant.
For two polygons to be similar, both conditions must be satisfied: corresponding angles must be equal, and corresponding sides must be proportional.
In this case, the corresponding angles are not equal, although the corresponding sides are proportional.
Therefore, the quadrilaterals PQRS (square) and ABCD (rhombus) are not similar.
Example 1 to 3 (Before Exercise 6.2)
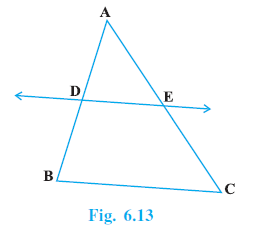
Example 1. If a line intersects sides AB and AC of a ∆ ABC at D and E respectively and is parallel to BC, prove that $\frac{AD}{AB}$ = $\frac{AE}{AC}$ (see Fig. 6.13).
Answer:
Given: In $\triangle ABC$, a line DE intersects AB at D and AC at E such that DE || BC.
To Prove: $\frac{AD}{AB} = \frac{AE}{AC}$.
Proof:
Consider $\triangle ADE$ and $\triangle ABC$.
$\angle ADE = \angle ABC$
(Corresponding angles, since DE || BC and AB is a transversal)
$\angle AED = \angle ACB$
(Corresponding angles, since DE || BC and AC is a transversal)
$\angle DAE = \angle BAC$
(Common angle to both triangles)
Since the corresponding angles of $\triangle ADE$ and $\triangle ABC$ are equal, by AAA similarity criterion, we have:
$\triangle ADE \sim \triangle ABC$.
When two triangles are similar, the ratio of their corresponding sides is equal.
Therefore, we can write:
$\frac{AD}{AB} = \frac{AE}{AC} = \frac{DE}{BC}$.
From the equality of the first two ratios, we get the required result:
$\frac{AD}{AB} = \frac{AE}{AC}$
Hence, proved.
Alternate Proof using Basic Proportionality Theorem (Theorem 6.1):
Given: In $\triangle ABC$, a line DE intersects AB at D and AC at E such that DE || BC.
To Prove: $\frac{AD}{AB} = \frac{AE}{AC}$.
Proof:
Since DE || BC, by the Basic Proportionality Theorem (BPT), also known as Thales' Theorem, if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
Therefore, we have:
$\frac{AD}{DB} = \frac{AE}{EC}$
(By BPT)
Now, we need to get the ratios $\frac{AD}{AB}$ and $\frac{AE}{AC}$. We can manipulate the equation $\frac{AD}{DB} = \frac{AE}{EC}$.
Take the reciprocal of both sides:
$\frac{DB}{AD} = \frac{EC}{AE}$.
Add 1 to both sides:
$\frac{DB}{AD} + 1 = \frac{EC}{AE} + 1$
$\frac{DB + AD}{AD} = \frac{EC + AE}{AE}$.
From the figure, $DB + AD = AB$ and $EC + AE = AC$. Substitute these into the equation:
$\frac{AB}{AD} = \frac{AC}{AE}$.
Take the reciprocal of both sides again:
$\frac{AD}{AB} = \frac{AE}{AC}$
Hence, proved.
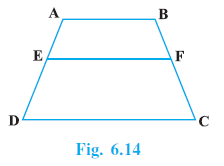
Example 2. ABCD is a trapezium with AB || DC. E and F are points on non-parallel sides AD and BC respectively such that EF is parallel to AB (see Fig. 6.14). Show that $\frac{AE}{ED}$ = $\frac{BF}{FC}$ .
Answer:
Given:
ABCD is a trapezium with $AB \parallel DC$.
E is a point on the non-parallel side AD.
F is a point on the non-parallel side BC.
$EF \parallel AB$.
Since $EF \parallel AB$ and $AB \parallel DC$, we also have $EF \parallel DC$. (Lines parallel to the same line are parallel to each other).
To Prove:
$\frac{AE}{ED} = \frac{BF}{FC}$
Construction:
Join AC, intersecting EF at point G.
Proof:
In $\triangle ADC$, we have EG on EF and DC.
Since $EF \parallel DC$, it implies $EG \parallel DC$.
Now, in $\triangle ADC$, by the Basic Proportionality Theorem (BPT) or Thales' Theorem, we have:
$\frac{AE}{ED} = \frac{AG}{GC}$
[By BPT as $EG \parallel DC$] ... (i)
In $\triangle CAB$, we have GF on EF and AB.
Since $EF \parallel AB$, it implies $GF \parallel AB$.
Now, in $\triangle CAB$, by the Basic Proportionality Theorem (BPT) or Thales' Theorem, we have:
$\frac{CG}{GA} = \frac{CF}{FB}$
[By BPT as $GF \parallel AB$]
Taking the reciprocal of the above equation:
$\frac{GA}{CG} = \frac{FB}{CF}$
$\frac{AG}{GC} = \frac{BF}{FC}$
... (ii)
From equation (i) and equation (ii), we get:
$\frac{AE}{ED} = \frac{BF}{FC}$
Hence Proved.
Alternate Solution:
Construction:
Join BD, intersecting EF at point H.
Proof:
In $\triangle DAB$, we have EH on EF and AB.
Since $EF \parallel AB$, it implies $EH \parallel AB$.
Now, in $\triangle DAB$, by the Basic Proportionality Theorem (BPT), we have:
$\frac{DE}{EA} = \frac{DH}{HB}$
[By BPT as $EH \parallel AB$]
Taking the reciprocal of the above equation:
$\frac{EA}{DE} = \frac{HB}{DH}$
$\frac{AE}{ED} = \frac{BH}{HD}$
... (iii)
In $\triangle BDC$, we have HF on EF and DC.
Since $EF \parallel DC$, it implies $HF \parallel DC$.
Now, in $\triangle BDC$, by the Basic Proportionality Theorem (BPT), we have:
$\frac{BH}{HD} = \frac{BF}{FC}$
[By BPT as $HF \parallel DC$] ... (iv)
From equation (iii) and equation (iv), we get:
$\frac{AE}{ED} = \frac{BF}{FC}$
Hence Proved.
Example 3. In Fig. 6.16, $\frac{PS}{SQ}$ = $\frac{PT}{TR}$ and ∠PST = ∠PRQ. Prove that PQR is an isosceles triangle.

Answer:
Given:
In $\triangle PQR$, points S and T are on sides PQ and PR respectively such that:
$\frac{PS}{SQ} = \frac{PT}{TR}$
(Given ratio)
$\angle PST = \angle PRQ$
(Given angles)
To Prove:
$\triangle PQR$ is an isosceles triangle.
Proof:
We are given that in $\triangle PQR$,
$\frac{PS}{SQ} = \frac{PT}{TR}$
(Given)
According to the Converse of the Basic Proportionality Theorem (BPT) (also known as Thales' Theorem), if a line divides any two sides of a triangle in the same ratio, then the line must be parallel to the third side.
Applying this theorem to $\triangle PQR$, since $\frac{PS}{SQ} = \frac{PT}{TR}$, we can conclude that:
$ST \parallel QR$
Now, consider the parallel lines $ST$ and $QR$ intersected by the transversal line $PQ$. The corresponding angles formed must be equal.
$\angle PST = \angle PQR$
[Corresponding angles] ... (i)
We are also given that:
$\angle PST = \angle PRQ$
[Given] ... (ii)
From equations (i) and (ii), we can equate the values of $\angle PST$:
$\angle PQR = \angle PRQ$
Now, consider $\triangle PQR$. We have found that two of its angles, $\angle PQR$ and $\angle PRQ$, are equal.
In a triangle, sides opposite to equal angles are equal in length.
Therefore, the side opposite to $\angle PRQ$ (which is PQ) must be equal to the side opposite to $\angle PQR$ (which is PR).
$PQ = PR$
A triangle with two equal sides is defined as an isosceles triangle.
Thus, $\triangle PQR$ is an isosceles triangle.
Hence Proved.
Exercise 6.2
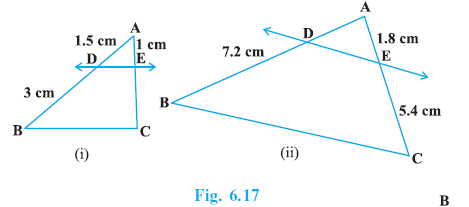
Question 1. In Fig. 6.17, (i) and (ii), DE || BC. Find EC in (i) and AD in (ii).
Answer:
Solution for (i)
Given:
In $\triangle ABC$, the line segment DE is parallel to the side BC ($DE \parallel BC$).
$AD = 1.5$ cm
$DB = 3$ cm
$AE = 1$ cm
To Find:
The length of EC.
Solution:
In $\triangle ABC$, we are given that $DE \parallel BC$.
By the Basic Proportionality Theorem (BPT), also known as Thales' Theorem, if a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio.
Therefore, we have:
$\frac{AD}{DB} = \frac{AE}{EC}$
[By BPT]
Substitute the given values into the equation:
$\frac{1.5}{3} = \frac{1}{EC}$
Now, we solve for EC:
$1.5 \times EC = 3 \times 1$
$1.5 \times EC = 3$
$EC = \frac{3}{1.5}$
$EC = \frac{30}{15}$
$EC = 2$
Thus, the length of EC is 2 cm.
Solution for (ii)
Given:
In $\triangle ABC$, the line segment DE is parallel to the side BC ($DE \parallel BC$).
$DB = 7.2$ cm
$AE = 1.8$ cm
$EC = 5.4$ cm
To Find:
The length of AD.
Solution:
In $\triangle ABC$, we are given that $DE \parallel BC$.
By the Basic Proportionality Theorem (BPT) or Thales' Theorem:
$\frac{AD}{DB} = \frac{AE}{EC}$
[By BPT]
Substitute the given values into the equation:
$\frac{AD}{7.2} = \frac{1.8}{5.4}$
Now, we solve for AD:
$AD = \frac{1.8}{5.4} \times 7.2$
Simplify the fraction $\frac{1.8}{5.4}$:
$\frac{1.8}{5.4} = \frac{18}{54} = \frac{\cancel{18}^{1}}{\cancel{54}_{3}} = \frac{1}{3}$
Substitute this back into the equation for AD:
$AD = \frac{1}{3} \times 7.2$
$AD = \frac{7.2}{3}$
$AD = 2.4$
Thus, the length of AD is 2.4 cm.
Question 2. E and F are points on the sides PQ and PR respectively of a ∆ PQR. For each of the following cases, state whether EF || QR :
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
Answer:
We need to check whether $EF \parallel QR$ in each case using the Converse of the Basic Proportionality Theorem (BPT). The theorem states that if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side. So, we need to check if $\frac{PE}{EQ} = \frac{PF}{FR}$ in each case.
Case (i)
Given:
$PE = 3.9$ cm
$EQ = 3$ cm
$PF = 3.6$ cm
$FR = 2.4$ cm
Calculation:
We calculate the ratios $\frac{PE}{EQ}$ and $\frac{PF}{FR}$.
$\frac{PE}{EQ} = \frac{3.9}{3} = \frac{39}{30} = \frac{\cancel{39}^{13}}{\cancel{30}_{10}} = \frac{13}{10} = 1.3$
$\frac{PF}{FR} = \frac{3.6}{2.4} = \frac{36}{24} = \frac{\cancel{36}^{3}}{\cancel{24}_{2}} = \frac{3}{2} = 1.5$
Conclusion:
Since $\frac{PE}{EQ} = 1.3$ and $\frac{PF}{FR} = 1.5$, the ratios are not equal.
$\frac{PE}{EQ} \neq \frac{PF}{FR}$
Therefore, by the Converse of BPT, EF is not parallel to QR.
Case (ii)
Given:
$PE = 4$ cm
$QE = 4.5$ cm
$PF = 8$ cm
$RF = 9$ cm
Calculation:
We calculate the ratios $\frac{PE}{QE}$ and $\frac{PF}{RF}$.
$\frac{PE}{QE} = \frac{4}{4.5} = \frac{40}{45} = \frac{\cancel{40}^{8}}{\cancel{45}_{9}} = \frac{8}{9}$
$\frac{PF}{RF} = \frac{8}{9}$
Conclusion:
Since $\frac{PE}{QE} = \frac{8}{9}$ and $\frac{PF}{RF} = \frac{8}{9}$, the ratios are equal.
$\frac{PE}{QE} = \frac{PF}{RF}$
Therefore, by the Converse of BPT, EF is parallel to QR.
Case (iii)
Given:
$PQ = 1.28$ cm
$PR = 2.56$ cm
$PE = 0.18$ cm
$PF = 0.36$ cm
Calculation:
First, we need to find the lengths of $EQ$ and $FR$.
$EQ = PQ - PE$
$\begin{array}{cc} & 1 & . & 2 & 8 \\ - & 0 & . & 1 & 8 \\ \hline & 1 & . & 1 & 0 \\ \hline \end{array}$
$EQ = 1.10$ cm
$FR = PR - PF$
$\begin{array}{cc} & 2 & . & 5 & 6 \\ - & 0 & . & 3 & 6 \\ \hline & 2 & . & 2 & 0 \\ \hline \end{array}$
$FR = 2.20$ cm
Now, we calculate the ratios $\frac{PE}{EQ}$ and $\frac{PF}{FR}$.
$\frac{PE}{EQ} = \frac{0.18}{1.10} = \frac{18}{110} = \frac{\cancel{18}^{9}}{\cancel{110}_{55}} = \frac{9}{55}$
$\frac{PF}{FR} = \frac{0.36}{2.20} = \frac{36}{220} = \frac{\cancel{36}^{9}}{\cancel{220}_{55}} = \frac{9}{55}$
Conclusion:
Since $\frac{PE}{EQ} = \frac{9}{55}$ and $\frac{PF}{FR} = \frac{9}{55}$, the ratios are equal.
$\frac{PE}{EQ} = \frac{PF}{FR}$
Therefore, by the Converse of BPT, EF is parallel to QR.
(Alternatively, we could check the ratios $\frac{PE}{PQ}$ and $\frac{PF}{PR}$:
$\frac{PE}{PQ} = \frac{0.18}{1.28} = \frac{18}{128} = \frac{\cancel{18}^{9}}{\cancel{128}_{64}} = \frac{9}{64}$
$\frac{PF}{PR} = \frac{0.36}{2.56} = \frac{36}{256} = \frac{\cancel{36}^{9}}{\cancel{256}_{64}} = \frac{9}{64}$
Since $\frac{PE}{PQ} = \frac{PF}{PR}$, by a corollary of the Converse of BPT, $EF \parallel QR$.)
Question 3. In Fig. 6.18, if LM || CB and LN || CD, prove that $\frac{AM}{AB}$ = $\frac{AN}{AD}$ .
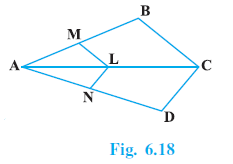
Answer:
Given:
In the given figure, we have:
$LM \parallel CB$
$LN \parallel CD$
To Prove:
$\frac{AM}{AB} = \frac{AN}{AD}$
Proof:
First, consider the triangle $\triangle ABC$.
We are given that $LM \parallel CB$.
By the Basic Proportionality Theorem (BPT) or Thales' Theorem, if a line is drawn parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio. A corollary of BPT states that the ratio of the parts to the whole sides are also equal.
Applying this corollary in $\triangle ABC$:
$\frac{AM}{AB} = \frac{AL}{AC}$
[Since $LM \parallel CB$] ... (i)
Next, consider the triangle $\triangle ADC$.
We are given that $LN \parallel CD$.
Applying the same corollary of BPT in $\triangle ADC$:
$\frac{AN}{AD} = \frac{AL}{AC}$
[Since $LN \parallel CD$] ... (ii)
From equation (i) and equation (ii), we observe that both $\frac{AM}{AB}$ and $\frac{AN}{AD}$ are equal to the same ratio $\frac{AL}{AC}$.
Therefore, we can equate them:
$\frac{AM}{AB} = \frac{AN}{AD}$
Hence Proved.
Question 4. In Fig. 6.19, DE || AC and DF || AE. Prove that $\frac{BF}{FE}$ = $\frac{BE}{EC}$ .

Answer:
Given:
In the given figure (presumably $\triangle ABC$ with points D on AB, E on BC, F on BE):
$DE \parallel AC$
$DF \parallel AE$
To Prove:
$\frac{BF}{FE} = \frac{BE}{EC}$
Proof:
First, consider the triangle $\triangle ABC$.
We are given that $DE \parallel AC$.
By the Basic Proportionality Theorem (BPT) or Thales' Theorem, if a line is drawn parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio.
Applying BPT in $\triangle ABC$ (considering line DE intersecting sides AB and BC):
$\frac{BD}{DA} = \frac{BE}{EC}$
[Since $DE \parallel AC$] ... (i)
Next, consider the triangle $\triangle ABE$.
We are given that $DF \parallel AE$.
Applying BPT in $\triangle ABE$ (considering line DF intersecting sides AB and BE):
$\frac{BD}{DA} = \frac{BF}{FE}$
[Since $DF \parallel AE$] ... (ii)
From equation (i) and equation (ii), we observe that both $\frac{BE}{EC}$ and $\frac{BF}{FE}$ are equal to the same ratio $\frac{BD}{DA}$.
Therefore, we can equate them:
$\frac{BF}{FE} = \frac{BE}{EC}$
Hence Proved.
Question 5. In Fig. 6.20, DE || OQ and DF || OR. Show that EF || QR.
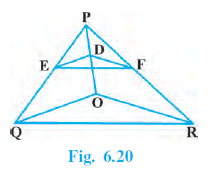
Answer:
Given:
In the given figure (presumably $\triangle PQR$ with point O inside, and points E on PQ, F on PR):
$DE \parallel OQ$
$DF \parallel OR$
To Prove:
$EF \parallel QR$
Proof:
First, consider the triangle $\triangle POQ$.
We are given that $DE \parallel OQ$.
By the Basic Proportionality Theorem (BPT), if a line is drawn parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio.
Applying BPT in $\triangle POQ$:
$\frac{PE}{EQ} = \frac{PD}{DO}$
[Since $DE \parallel OQ$] ... (i)
Next, consider the triangle $\triangle POR$.
We are given that $DF \parallel OR$.
Applying BPT in $\triangle POR$:
$\frac{PF}{FR} = \frac{PD}{DO}$
[Since $DF \parallel OR$] ... (ii)
From equation (i) and equation (ii), we observe that both $\frac{PE}{EQ}$ and $\frac{PF}{FR}$ are equal to the same ratio $\frac{PD}{DO}$.
Therefore, we can equate them:
$\frac{PE}{EQ} = \frac{PF}{FR}$
Now, consider the triangle $\triangle PQR$.
We have found that the line segment EF divides the sides PQ and PR in the same ratio, i.e., $\frac{PE}{EQ} = \frac{PF}{FR}$.
By the Converse of the Basic Proportionality Theorem (Converse of BPT), if a line divides any two sides of a triangle in the same ratio, then the line must be parallel to the third side.
Applying the Converse of BPT in $\triangle PQR$:
$EF \parallel QR$
Hence Proved.
Question 6. In Fig. 6.21, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.
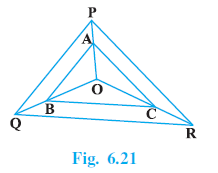
Answer:
Given:
In the given figure:
A is a point on OP.
B is a point on OQ.
C is a point on OR.
$AB \parallel PQ$
$AC \parallel PR$
To Prove:
$BC \parallel QR$
Proof:
First, consider the triangle $\triangle OPQ$.
We are given that $AB \parallel PQ$.
By the Basic Proportionality Theorem (BPT) or Thales' Theorem (using the corollary regarding ratios involving the whole side):
$\frac{OA}{OP} = \frac{OB}{OQ}$
[Since $AB \parallel PQ$] ... (i)
Next, consider the triangle $\triangle OPR$.
We are given that $AC \parallel PR$.
Applying the same corollary of BPT in $\triangle OPR$:
$\frac{OA}{OP} = \frac{OC}{OR}$
[Since $AC \parallel PR$] ... (ii)
From equation (i) and equation (ii), we observe that both $\frac{OB}{OQ}$ and $\frac{OC}{OR}$ are equal to the same ratio $\frac{OA}{OP}$.
Therefore, we can equate them:
$\frac{OB}{OQ} = \frac{OC}{OR}$
Now, consider the triangle $\triangle OQR$.
We have found that the line segment BC divides the sides OQ and OR such that $\frac{OB}{OQ} = \frac{OC}{OR}$.
By the Converse of the Basic Proportionality Theorem (Converse of BPT), if a line divides any two sides of a triangle proportionally (i.e., the ratios $\frac{\text{part}}{\text{whole side}}$ are equal), then the line must be parallel to the third side.
Applying the Converse of BPT (corollary form) in $\triangle OQR$:
Since $\frac{OB}{OQ} = \frac{OC}{OR}$, we conclude that $BC \parallel QR$.
Hence Proved.
Question 7. Using Theorem 6.1, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX).
Answer:
Statement: To prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side, using Theorem 6.1 (Basic Proportionality Theorem).
Given:
A triangle $\triangle ABC$.
D is the mid-point of side AB. This means $AD = DB$.
A line DE is drawn through D such that $DE \parallel BC$, and DE intersects side AC at point E.
To Prove:
E is the mid-point of side AC. (i.e., $AE = EC$).
Proof:
In $\triangle ABC$, we are given that the line segment DE is drawn parallel to the side BC.
$DE \parallel BC$
According to Theorem 6.1 (Basic Proportionality Theorem - BPT), if a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio.
Applying BPT to $\triangle ABC$ with $DE \parallel BC$, we get:
$\frac{AD}{DB} = \frac{AE}{EC}$
[By BPT] ... (i)
We are also given that D is the mid-point of side AB.
$AD = DB$
[Given]
Dividing both sides by DB (since $DB \neq 0$), we get:
$\frac{AD}{DB} = 1$
... (ii)
Now, substituting the value from equation (ii) into equation (i):
$1 = \frac{AE}{EC}$
Cross-multiplying, we get:
$AE = EC$
Since AE is equal to EC, the point E divides the side AC into two equal parts.
Therefore, E is the mid-point of the side AC.
This proves that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side.
Hence Proved.
Question 8. Using Theorem 6.2, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX).
Answer:
Statement: To prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side, using Theorem 6.2 (Converse of Basic Proportionality Theorem).
Given:
A triangle $\triangle ABC$.
D is the mid-point of side AB. This means $AD = DB$.
E is the mid-point of side AC. This means $AE = EC$.
DE is the line segment joining the mid-points D and E.
To Prove:
$DE \parallel BC$.
Proof:
Since D is the mid-point of AB, we have:
$AD = DB$
[Definition of mid-point]
Dividing both sides by DB (since $DB \neq 0$), we get:
$\frac{AD}{DB} = 1$
... (i)
Since E is the mid-point of AC, we have:
$AE = EC$
[Definition of mid-point]
Dividing both sides by EC (since $EC \neq 0$), we get:
$\frac{AE}{EC} = 1$
... (ii)
From equation (i) and equation (ii), we can see that:
$\frac{AD}{DB} = \frac{AE}{EC}$
Now, consider the triangle $\triangle ABC$. The line segment DE intersects the sides AB and AC such that it divides these sides in the same ratio ($\frac{AD}{DB} = \frac{AE}{EC}$).
According to Theorem 6.2 (Converse of the Basic Proportionality Theorem - Converse of BPT), if a line divides any two sides of a triangle in the same ratio, then the line must be parallel to the third side.
Applying Theorem 6.2 to $\triangle ABC$:
Since $\frac{AD}{DB} = \frac{AE}{EC}$, we can conclude that the line segment DE is parallel to the third side BC.
$DE \parallel BC$
This proves that the line joining the mid-points of any two sides of a triangle is parallel to the third side.
Hence Proved.
Question 9. ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that $\frac{AO}{BO}$ = $\frac{CO}{DO}$
Answer:
Given:
A trapezium ABCD in which side $AB$ is parallel to side $DC$ ($AB \parallel DC$).
The diagonals AC and BD intersect each other at the point O.
To Prove:
$\frac{AO}{BO} = \frac{CO}{DO}$
Proof (Using Similar Triangles):
Consider the triangles $\triangle AOB$ and $\triangle COD$.
Since $AB \parallel DC$ and AC is a transversal line:
$\angle OAB = \angle OCD$
[Alternate interior angles]
Also written as $\angle BAC = \angle DCA$
Since $AB \parallel DC$ and BD is a transversal line:
$\angle OBA = \angle ODC$
[Alternate interior angles]
Also written as $\angle ABD = \angle CDB$
Also, the angles formed at the intersection O:
$\angle AOB = \angle COD$
[Vertically opposite angles]
Therefore, by the AAA (Angle-Angle-Angle) similarity criterion, the two triangles are similar:
$\triangle AOB \sim \triangle COD$
Since the triangles are similar, the ratio of their corresponding sides must be equal.
Corresponding sides are (AO with CO), (BO with DO), and (AB with CD).
$\frac{AO}{CO} = \frac{BO}{DO} = \frac{AB}{CD}$
[Ratio of corresponding sides of similar triangles]
From the first two parts of the equality, we have:
$\frac{AO}{CO} = \frac{BO}{DO}$
Rearranging the terms (using alternendo property of proportions, or by cross-multiplication and rearranging):
$AO \times DO = BO \times CO$
Divide both sides by $BO \times DO$ (assuming $BO, DO \neq 0$):
$\frac{AO \times \cancel{DO}}{BO \times \cancel{DO}} = \frac{\cancel{BO} \times CO}{\cancel{BO} \times DO}$
$\frac{AO}{BO} = \frac{CO}{DO}$
Hence Proved.
Alternate Proof (Using BPT):
Construction:
Draw a line segment OE through O parallel to AB, such that E lies on AD.
$OE \parallel AB$
Since $AB \parallel DC$ (Given) and $OE \parallel AB$ (Construction), we have $OE \parallel DC$.
Proof:
Consider $\triangle ADC$.
We have $OE \parallel DC$ (from construction and given). E lies on AD and O lies on AC.
By the Basic Proportionality Theorem (BPT):
$\frac{AE}{ED} = \frac{AO}{CO}$
[By BPT in $\triangle ADC$] ... (i)
Now consider $\triangle DAB$.
We have $OE \parallel AB$ (from construction). E lies on AD and O lies on BD.
By the Basic Proportionality Theorem (BPT):
$\frac{DE}{EA} = \frac{DO}{OB}$
[By BPT in $\triangle DAB$]
Taking the reciprocal of both sides:
$\frac{EA}{DE} = \frac{OB}{DO}$
$\frac{AE}{ED} = \frac{BO}{DO}$
... (ii)
From equation (i) and equation (ii), we can equate the expressions for $\frac{AE}{ED}$:
$\frac{AO}{CO} = \frac{BO}{DO}$
Rearranging the terms:
$\frac{AO}{BO} = \frac{CO}{DO}$
Hence Proved.
Question 10. The diagonals of a quadrilateral ABCD intersect each other at the point O such that $\frac{AO}{BO}$ = $\frac{CO}{DO}$
Answer:
Given:
A quadrilateral ABCD.
The diagonals AC and BD intersect each other at the point O.
$\frac{AO}{BO} = \frac{CO}{DO}$
To Prove:
ABCD is a trapezium (which means we need to show that one pair of opposite sides is parallel, typically $AB \parallel DC$).
Construction:
Draw a line segment OE through the point O such that OE is parallel to AB, and E lies on the side AD.
$OE \parallel AB$
Proof:
We are given the ratio:
$\frac{AO}{BO} = \frac{CO}{DO}$
Rearranging this equation (using alternendo or cross-multiplication), we get:
$\frac{AO}{CO} = \frac{BO}{DO}$
... (i)
Now, consider the triangle $\triangle DAB$.
By construction, we have $OE \parallel AB$.
Applying the Basic Proportionality Theorem (BPT) to $\triangle DAB$:
$\frac{DE}{EA} = \frac{DO}{OB}$
[By BPT as $OE \parallel AB$]
Taking the reciprocal of both sides:
$\frac{EA}{DE} = \frac{OB}{DO}$
$\frac{AE}{ED} = \frac{BO}{DO}$
... (ii)
Comparing equation (i) and equation (ii):
From (i), $\frac{BO}{DO} = \frac{AO}{CO}$.
Substituting this into (ii):
$\frac{AE}{ED} = \frac{AO}{CO}$
Now, consider the triangle $\triangle ADC$.
The line segment OE intersects the sides AD and AC at points E and O respectively, such that the ratio $\frac{AE}{ED}$ is equal to the ratio $\frac{AO}{CO}$.
By the Converse of the Basic Proportionality Theorem (Converse of BPT), if a line divides any two sides of a triangle in the same ratio, then the line must be parallel to the third side.
Applying the Converse of BPT to $\triangle ADC$:
Since $\frac{AE}{ED} = \frac{AO}{CO}$, we conclude that $OE \parallel DC$.
So, we have:
$OE \parallel AB$ (By Construction)
$OE \parallel DC$ (Proved above)
Since the line segment OE is parallel to both AB and DC, it means that AB and DC must be parallel to each other.
$AB \parallel DC$
A quadrilateral with at least one pair of opposite sides parallel is called a trapezium.
Therefore, the quadrilateral ABCD is a trapezium.
Hence Proved.
Example 4 to 8 (Before Exercise 6.3)
Example 4. In Fig. 6.29, if PQ || RS, prove that ∆ POQ ~ ∆ SOR

Answer:
Given:
We are given a figure where line segments PQ and RS are parallel ($PQ \parallel RS$).
Line segments PR and QS intersect each other at point O.
To Prove:
$\triangle POQ \sim \triangle SOR$ (Triangle POQ is similar to triangle SOR).
Proof:
We need to compare the angles of $\triangle POQ$ and $\triangle SOR$.
Consider the parallel lines PQ and RS, and the transversal line PR.
Since $PQ \parallel RS$ and PR is a transversal:
$\angle OPQ = \angle ORS$
[Alternate interior angles]
Also written as $\angle P = \angle R$ within the context of these triangles.
Consider the parallel lines PQ and RS, and the transversal line QS.
Since $PQ \parallel RS$ and QS is a transversal:
$\angle OQP = \angle OSR$
[Alternate interior angles]
Also written as $\angle Q = \angle S$ within the context of these triangles.
Now consider the angles at the intersection point O.
The lines PR and QS intersect at O.
$\angle POQ = \angle SOR$
[Vertically opposite angles]
In $\triangle POQ$ and $\triangle SOR$, we have found that:
$\angle OPQ = \angle ORS$
$\angle OQP = \angle OSR$
$\angle POQ = \angle SOR$
Since all three corresponding angles of $\triangle POQ$ are equal to the corresponding angles of $\triangle SOR$, the two triangles are similar by the AAA (Angle-Angle-Angle) similarity criterion.
(Alternatively, showing any two pairs of corresponding angles are equal is sufficient by the AA similarity criterion).
Therefore,
$\triangle POQ \sim \triangle SOR$
Hence Proved.
Example 5. Observe Fig. 6.30 and then find ∠P.

Answer:
Given:
Two triangles, $\triangle ABC$ and $\triangle PQR$, with the following measurements:
In $\triangle ABC$:
$AB = 3.8$
$BC = 6$
$AC = 3\sqrt{3}$
$\angle A = 80^\circ$
$\angle B = 60^\circ$
In $\triangle PQR$:
$RP = 7.6$
$QR = 12$
$PQ = 6\sqrt{3}$
To Find:
The measure of $\angle P$.
Solution:
First, let's check if the two triangles are similar by comparing the ratios of their corresponding sides. We need to find the correct correspondence between the vertices.
Let's calculate the ratios of the sides:
Comparing side AB with RP:
$\frac{AB}{RP} = \frac{3.8}{7.6} = \frac{38}{76} = \frac{1}{2}$
Comparing side BC with QR:
$\frac{BC}{QR} = \frac{6}{12} = \frac{1}{2}$
Comparing side AC with PQ:
$\frac{AC}{PQ} = \frac{3\sqrt{3}}{6\sqrt{3}} = \frac{3}{6} = \frac{1}{2}$
Since the ratios of the corresponding sides are equal:
$\frac{AB}{RP} = \frac{BC}{QR} = \frac{AC}{PQ} = \frac{1}{2}$
By the SSS (Side-Side-Side) similarity criterion, the two triangles are similar.
The correspondence of vertices is $A \leftrightarrow R$, $B \leftrightarrow Q$, and $C \leftrightarrow P$.
Therefore, we can write the similarity as:
$\triangle ABC \sim \triangle RQP$
Since the triangles are similar, their corresponding angles must be equal.
$\angle A = \angle R$
$\angle B = \angle Q$
$\angle C = \angle P$
We need to find $\angle P$, which is equal to $\angle C$.
We can find $\angle C$ using the angle sum property of a triangle in $\triangle ABC$. The sum of angles in a triangle is $180^\circ$.
$\angle A + \angle B + \angle C = 180^\circ$
Substitute the given values of $\angle A$ and $\angle B$:
$80^\circ + 60^\circ + \angle C = 180^\circ$
$140^\circ + \angle C = 180^\circ$
$\angle C = 180^\circ - 140^\circ$
$\angle C = 40^\circ$
Since $\angle P = \angle C$, we have:
$\angle P = 40^\circ$
Thus, the measure of $\angle P$ is 40°.
Example 6. In Fig. 6.31,
OA . OB = OC . OD.
Show that ∠A = ∠C and ∠B = ∠D.
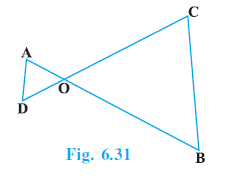
Answer:
Given:
In the given figure, lines AC and BD intersect at point O such that:
$OA \cdot OB = OC \cdot OD$
(Given condition)
To Prove:
$\angle A = \angle C$ (which means $\angle OAD = \angle OCB$)
and
$\angle B = \angle D$ (which means $\angle OBC = \angle ODA$)
Proof:
We are given the relation:
$OA \cdot OB = OC \cdot OD$
We can rearrange this equation to form ratios of sides. Divide both sides by $OC \cdot OB$ (assuming $OC \neq 0$ and $OB \neq 0$):
$\frac{OA \cdot \cancel{OB}}{OC \cdot \cancel{OB}} = \frac{\cancel{OC} \cdot OD}{\cancel{OC} \cdot OB}$
$\frac{OA}{OC} = \frac{OD}{OB}$
... (i)
Now, consider the triangles $\triangle AOD$ and $\triangle COB$.
From equation (i), we have the ratio of two pairs of corresponding sides:
$\frac{OA}{OC} = \frac{OD}{OB}$
Consider the angle included between these sides in each triangle.
In $\triangle AOD$, the angle included between sides OA and OD is $\angle AOD$.
In $\triangle COB$, the angle included between sides OC and OB is $\angle COB$.
We know that when two lines intersect, the vertically opposite angles formed are equal.
$\angle AOD = \angle COB$
[Vertically opposite angles] ... (ii)
Now we have two pairs of corresponding sides in proportion (from eq. (i)) and the included angles equal (from eq. (ii)).
Therefore, by the SAS (Side-Angle-Side) similarity criterion, the two triangles are similar:
$\triangle AOD \sim \triangle COB$
Since the triangles are similar, their corresponding angles must be equal.
The correspondence is $A \leftrightarrow C$, $O \leftrightarrow O$, $D \leftrightarrow B$.
Therefore:
$\angle OAD = \angle OCB$
[Corresponding angles of similar triangles]
This implies $\angle A = \angle C$.
And:
$\angle ODA = \angle OBC$
[Corresponding angles of similar triangles]
This implies $\angle D = \angle B$.
Thus, we have shown that $\angle A = \angle C$ and $\angle B = \angle D$.
Hence Proved.
Example 7. A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2 m/s. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.
Answer:
Given:
Height of the lamp-post (AB) = 3.6 m
Height of the girl (CD) = 90 cm = 0.9 m (since 1 m = 100 cm)
Speed of the girl = 1.2 m/s
Time = 4 seconds
The girl is walking away from the base of the lamp-post.
To Find:
The length of the girl's shadow after 4 seconds.
Solution:
Let AB represent the lamp-post and CD represent the girl. Assume both are standing vertically on the ground.
Let B be the base of the lamp-post and D be the position of the girl's feet after 4 seconds.
The distance walked by the girl in 4 seconds is:
Distance = Speed $\times$ Time
$BD = 1.2 \, \text{m/s} \times 4 \, \text{s} = 4.8 \, \text{m}$
Let DE be the length of the girl's shadow. Let $DE = x$ meters.
The shadow is formed by the light from the lamp (A) passing over the girl's head (C) and hitting the ground at point E.
We can visualize two right-angled triangles: $\triangle ABE$ and $\triangle CDE$.
In $\triangle ABE$ and $\triangle CDE$:
$\angle ABE = \angle CDE = 90^\circ$
[Both lamp-post and girl are vertical to the ground]
$\angle AEB = \angle CED$
[Common angle E]
Therefore, by the AA (Angle-Angle) similarity criterion, the two triangles are similar:
$\triangle ABE \sim \triangle CDE$
Since the triangles are similar, the ratio of their corresponding sides must be equal.
$\frac{AB}{CD} = \frac{BE}{DE}$
We know:
$AB = 3.6$ m
$CD = 0.9$ m
$DE = x$ m
$BE = BD + DE = 4.8 + x$ m
Substitute these values into the proportion:
$\frac{3.6}{0.9} = \frac{4.8 + x}{x}$
Simplify the left side:
$\frac{3.6}{0.9} = \frac{36}{9} = 4$
So the equation becomes:
$4 = \frac{4.8 + x}{x}$
Multiply both sides by $x$ (assuming $x \neq 0$):
$4x = 4.8 + x$
Subtract $x$ from both sides:
$4x - x = 4.8$
$3x = 4.8$
Divide by 3:
$x = \frac{4.8}{3}$
$x = 1.6$
Therefore, the length of the girl's shadow (DE) after 4 seconds is 1.6 meters.
Example 8. In Fig. 6.33, CM and RN are respectively the medians of ∆ ABC and ∆ PQR. If ∆ ABC ~ ∆ PQR, prove that :
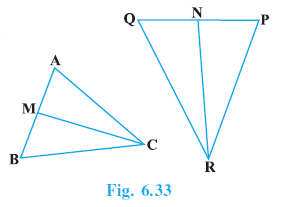
(i) ∆ AMC ~ ∆ PNR
(ii) $\frac{CN}{RN}$ = $\frac{AB}{PQ}$
(iii) ∆ CMB ~ ∆ RNQ
Answer:
Given:
$\triangle ABC \sim \triangle PQR$.
CM is the median of $\triangle ABC$ to side AB. (M is the midpoint of AB, so $AM = MB = \frac{1}{2}AB$).
RN is the median of $\triangle PQR$ to side PQ. (N is the midpoint of PQ, so $PN = NQ = \frac{1}{2}PQ$).
To Prove:
(i) $\triangle AMC \sim \triangle PNR$
(ii) $\frac{CM}{RN} = \frac{AB}{PQ}$
(iii) $\triangle CMB \sim \triangle RNQ$
Proof:
Since $\triangle ABC \sim \triangle PQR$, we know that their corresponding angles are equal and the ratios of their corresponding sides are equal.
$\angle A = \angle P, \; \angle B = \angle Q, \; \angle C = \angle R$
... (a)
$\frac{AB}{PQ} = \frac{BC}{QR} = \frac{CA}{RP}$
... (b)
Also, since CM and RN are medians:
$AM = MB = \frac{1}{2}AB$
... (c)
$PN = NQ = \frac{1}{2}PQ$
... (d)
(i) Prove $\triangle AMC \sim \triangle PNR$
Consider $\triangle AMC$ and $\triangle PNR$.
From (a), we have:
$\angle A = \angle P$
(Angle)
From (b), we have $\frac{AB}{PQ} = \frac{CA}{RP}$.
Using (c) and (d), we can write AB and PQ in terms of their halves:
$AB = 2AM$ and $PQ = 2PN$.
Substitute these into the ratio:
$\frac{2AM}{2PN} = \frac{CA}{RP}$
$\frac{AM}{PN} = \frac{AC}{PR}$
$\frac{AM}{PN} = \frac{AC}{PR}$
(Ratio of sides)
So, in $\triangle AMC$ and $\triangle PNR$, we have one pair of angles equal ($\angle A = \angle P$) and the ratio of the sides including these angles is equal ($\frac{AM}{PN} = \frac{AC}{PR}$).
Therefore, by the SAS (Side-Angle-Side) similarity criterion:
$\triangle AMC \sim \triangle PNR$
Hence Proved (i).
(ii) Prove $\frac{CM}{RN} = \frac{AB}{PQ}$
From part (i), we proved that $\triangle AMC \sim \triangle PNR$.
Since the triangles are similar, the ratio of their corresponding sides is equal:
$\frac{AM}{PN} = \frac{MC}{NR} = \frac{CA}{RP}$
Considering the first two parts of the equality:
$\frac{AM}{PN} = \frac{CM}{RN}$
From (c) and (d), substitute $AM = \frac{1}{2}AB$ and $PN = \frac{1}{2}PQ$:
$\frac{\frac{1}{2}AB}{\frac{1}{2}PQ} = \frac{CM}{RN}$
$\frac{AB}{PQ} = \frac{CM}{RN}$
Or, written as requested:
$\frac{CM}{RN} = \frac{AB}{PQ}$
Hence Proved (ii).
(iii) Prove $\triangle CMB \sim \triangle RNQ$
Consider $\triangle CMB$ and $\triangle RNQ$.
From (a), we have:
$\angle B = \angle Q$
(Angle)
From (b), we have $\frac{AB}{PQ} = \frac{BC}{QR}$.
Using (c) and (d), we can write AB and PQ in terms of their other halves:
$AB = 2MB$ and $PQ = 2NQ$.
Substitute these into the ratio:
$\frac{2MB}{2NQ} = \frac{BC}{QR}$
$\frac{MB}{NQ} = \frac{BC}{QR}$
$\frac{MB}{NQ} = \frac{BC}{QR}$
(Ratio of sides)
So, in $\triangle CMB$ and $\triangle RNQ$, we have one pair of angles equal ($\angle B = \angle Q$) and the ratio of the sides including these angles is equal ($\frac{MB}{NQ} = \frac{BC}{QR}$).
Therefore, by the SAS (Side-Angle-Side) similarity criterion:
$\triangle CMB \sim \triangle RNQ$
Hence Proved (iii).
Exercise 6.3
Question 1. State which pairs of triangles in Fig. 6.34 are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :
(i)
.png)
(ii)
.png)
(iii)
.png)
(iv)
.png)
(v)
.png)
(vi)
.png)
Answer:
(i)
Comparison:
In $\triangle ABC$ and $\triangle PQR$:
$\angle A = \angle P = 60^\circ$
$\angle B = \angle Q = 80^\circ$
$\angle C = \angle R = 40^\circ$
Conclusion:
Since all corresponding angles are equal, the triangles are similar.
Criterion:
AAA similarity criterion.
Symbolic Form:
$\triangle ABC \sim \triangle PQR$.
(ii)
Comparison:
In $\triangle ABC$ and $\triangle QRP$:
Consider the ratios of corresponding sides:
$\frac{AB}{QR} = \frac{2}{4} = \frac{1}{2}$
$\frac{BC}{RP} = \frac{2.5}{5} = \frac{25}{50} = \frac{1}{2}$
$\frac{CA}{PQ} = \frac{3}{6} = \frac{1}{2}$
Conclusion:
Since the ratios of all corresponding sides are equal ($\frac{AB}{QR} = \frac{BC}{RP} = \frac{CA}{PQ}$), the triangles are similar.
Criterion:
SSS similarity criterion.
Symbolic Form:
$\triangle ABC \sim \triangle QRP$.
(iii)
Comparison:
In $\triangle LMP$ and $\triangle DEF$:
Consider the ratios of corresponding sides (matching shortest to shortest, longest to longest, etc.):
Shortest sides: $\frac{MP}{DE} = \frac{2}{4} = \frac{1}{2}$
Longest sides: $\frac{LP}{DF} = \frac{3}{6} = \frac{1}{2}$
Middle sides: $\frac{LM}{EF} = \frac{2.7}{5} = \frac{27}{50}$
Conclusion:
Since the ratios of corresponding sides are not all equal ($\frac{MP}{DE} = \frac{LP}{DF} \neq \frac{LM}{EF}$), the triangles are not similar.
(iv)
Comparison:
In $\triangle MNL$ and $\triangle QPR$:
Consider the angle and the sides including it:
$\angle M = \angle Q = 70^\circ$ (Given angle)
Check the ratio of the sides including these angles:
$\frac{MN}{QP} = \frac{2.5}{5} = \frac{25}{50} = \frac{1}{2}$
$\frac{ML}{QR} = \frac{5}{10} = \frac{1}{2}$
Conclusion:
Since one angle is equal in both triangles and the ratios of the sides including these angles are equal ($\frac{MN}{QP} = \frac{ML}{QR}$), the triangles are similar.
Criterion:
SAS similarity criterion.
Symbolic Form:
$\triangle MNL \sim \triangle QPR$.
(v)
Comparison:
In $\triangle ABC$ and $\triangle FDE$:
We are given $AB = 2.5$, $BC = 3$, $\angle A = 80^\circ$ in $\triangle ABC$.
We are given $EF = 6$, $DE = 5$, $\angle F = 80^\circ$ in $\triangle DEF$.
Let's check SAS similarity with the given angle $\angle A = \angle F = 80^\circ$.
The sides including $\angle A$ are AB and AC. $AB = 2.5$. AC is unknown.
The sides including $\angle F$ are FE and FD. $FE = 6$. FD is unknown.
The ratio $\frac{AB}{FE} = \frac{2.5}{6} = \frac{25}{60} = \frac{5}{12}$.
We don't know the ratio $\frac{AC}{FD}$.
Alternatively, consider the given sides $AB=2.5, BC=3$ and $DE=5, EF=6$.
$\frac{AB}{DE} = \frac{2.5}{5} = \frac{1}{2}$
$\frac{BC}{EF} = \frac{3}{6} = \frac{1}{2}$
The sides are in proportion. For SAS similarity, the included angle should be equal. The angle included between AB and BC is $\angle B$. The angle included between DE and EF is $\angle E$. We don't know if $\angle B = \angle E$. We are given $\angle A=80^\circ$ and $\angle F=80^\circ$. The given angle $\angle A$ is not included between the sides AB and BC. The given angle $\angle F$ is not included between sides DE and EF.
Conclusion:
The conditions for SAS similarity are not met with the given information. The triangles are not similar based on the provided data.
(vi)
Comparison:
In $\triangle DEF$:
$\angle D = 70^\circ$, $\angle E = 80^\circ$
$\angle F = 180^\circ - (70^\circ + 80^\circ) = 180^\circ - 150^\circ = 30^\circ$
In $\triangle PQR$:
$\angle Q = 80^\circ$, $\angle R = 30^\circ$
$\angle P = 180^\circ - (80^\circ + 30^\circ) = 180^\circ - 110^\circ = 70^\circ$
Comparing angles:
$\angle D = \angle P = 70^\circ$
$\angle E = \angle Q = 80^\circ$
$\angle F = \angle R = 30^\circ$
Conclusion:
Since all corresponding angles are equal, the triangles are similar.
Criterion:
AAA similarity criterion (or AA similarity criterion).
Symbolic Form:
$\triangle DEF \sim \triangle PQR$.
Question 2. In Fig. 6.35, ∆ ODC ~ ∆ OBA, ∠BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO and ∠OAB.
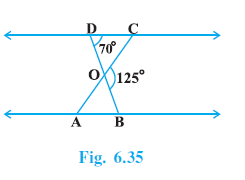
Answer:
Given:
In Fig. 6.35:
$\triangle ODC \sim \triangle OBA$
DOB is a straight line.
$\angle BOC = 125^\circ$
$\angle CDO = 70^\circ$
To Find:
$\angle DOC$
$\angle DCO$
$\angle OAB$
Solution:
1. Finding $\angle DOC$:
Since DOB is a straight line, the angles $\angle DOC$ and $\angle BOC$ form a linear pair.
The sum of angles in a linear pair is $180^\circ$.
$\angle DOC + \angle BOC = 180^\circ$
[Linear Pair Axiom]
Substitute the given value $\angle BOC = 125^\circ$:
$\angle DOC + 125^\circ = 180^\circ$
$\angle DOC = 180^\circ - 125^\circ$
$\angle DOC = 55^\circ$
2. Finding $\angle DCO$:
Consider the triangle $\triangle ODC$.
The sum of the interior angles of a triangle is $180^\circ$.
$\angle DOC + \angle CDO + \angle DCO = 180^\circ$
[Angle sum property of a triangle]
Substitute the known values $\angle DOC = 55^\circ$ and $\angle CDO = 70^\circ$:
$55^\circ + 70^\circ + \angle DCO = 180^\circ$
$125^\circ + \angle DCO = 180^\circ$
$\angle DCO = 180^\circ - 125^\circ$
$\angle DCO = 55^\circ$
3. Finding $\angle OAB$:
We are given that the triangles are similar:
$\triangle ODC \sim \triangle OBA$
In similar triangles, corresponding angles are equal.
The correspondence is $O \leftrightarrow O$, $D \leftrightarrow B$, $C \leftrightarrow A$.
Therefore, the corresponding angles are:
$\angle DOC = \angle BOA$
$\angle CDO = \angle ABO$
$\angle DCO = \angle OAB$
We need to find $\angle OAB$. From the correspondence, we have:
$\angle OAB = \angle DCO$
[Corresponding angles of similar triangles]
From step 2, we found $\angle DCO = 55^\circ$.
Therefore, $\angle OAB = 55^\circ$.
Summary of Results:
$\angle DOC = 55^\circ$
$\angle DCO = 55^\circ$
$\angle OAB = 55^\circ$
Question 3. Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that $\frac{OA}{OC}$ = $\frac{OB}{OD}$ .
Answer:
Given:
A trapezium ABCD.
Side $AB \parallel$ side $DC$.
Diagonals AC and BD intersect each other at point O.
To Prove:
$\frac{OA}{OC} = \frac{OB}{OD}$ using a similarity criterion.
Proof:
We need to show the required ratio by proving the similarity of two triangles whose sides are involved in the ratio. Consider the triangles $\triangle AOB$ and $\triangle COD$.
Since $AB \parallel DC$, we can analyze the angles formed by the transversals AC and BD.
Consider transversal AC intersecting the parallel lines AB and DC:
$\angle OAB = \angle OCD$
[Alternate interior angles]
(Also written as $\angle CAB = \angle ACD$)
Consider transversal BD intersecting the parallel lines AB and DC:
$\angle OBA = \angle ODC$
[Alternate interior angles]
(Also written as $\angle DBA = \angle BDC$)
Also, consider the angles at the intersection point O:
$\angle AOB = \angle COD$
[Vertically opposite angles]
Now, in $\triangle AOB$ and $\triangle COD$, we have:
$\angle OAB = \angle OCD$
$\angle OBA = \angle ODC$
$\angle AOB = \angle COD$
By the AAA (Angle-Angle-Angle) similarity criterion (or simply by the AA similarity criterion using any two pairs of equal angles), the two triangles are similar.
$\triangle AOB \sim \triangle COD$
Since the triangles are similar, the ratio of their corresponding sides must be equal. The correspondence of vertices is $A \leftrightarrow C$, $O \leftrightarrow O$, $B \leftrightarrow D$.
Therefore, we can write the ratios:
$\frac{OA}{OC} = \frac{OB}{OD} = \frac{AB}{CD}$
[Ratio of corresponding sides of similar triangles]
From this equality, we can take the part we need to prove:
$\frac{OA}{OC} = \frac{OB}{OD}$
Hence Proved.
Question 4. In fig. 6.36, $\frac{QR}{QS}$ = $\frac{QT}{PR}$ and ∠1 = ∠2. Show that ∆ PQS ~ ∆ TQR.
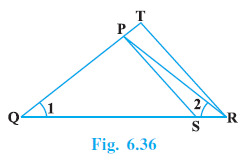
Answer:
Given:
In the figure (presumably $\triangle TQR$ with point P on TQ and point S on QR):
$\frac{QR}{QS} = \frac{QT}{PR}$
... (i)
$\angle 1 = \angle 2$
(Where $\angle 1 = \angle PQR$ and $\angle 2 = \angle PRQ$)
To Prove:
$\triangle PQS \sim \triangle TQR$
Proof:
First, consider the triangle $\triangle PQR$.
We are given that $\angle 1 = \angle 2$.
In $\triangle PQR$, $\angle PQR = \angle 1$ and $\angle PRQ = \angle 2$.
Therefore, $\angle PQR = \angle PRQ$.
In a triangle, sides opposite to equal angles are equal in length.
The side opposite to $\angle PRQ$ is PQ.
The side opposite to $\angle PQR$ is PR.
Hence, $PQ = PR$.
$PQ = PR$
[Sides opposite equal angles in $\triangle PQR$] ... (ii)
Now substitute the result from (ii) into the given ratio (i):
Given: $\frac{QR}{QS} = \frac{QT}{PR}$
Substituting $PR = PQ$:
$\frac{QR}{QS} = \frac{QT}{PQ}$
Rearranging this equation to match the sides of the triangles we want to prove similar ($\triangle PQS$ and $\triangle TQR$):
Cross-multiply: $QR \cdot PQ = QS \cdot QT$
Divide both sides by $QT \cdot QR$:
$\frac{PQ}{QT} = \frac{QS}{QR}$
$\frac{PQ}{QT} = \frac{QS}{QR}$
... (iii)
Now, consider the triangles $\triangle PQS$ and $\triangle TQR$.
From equation (iii), we have the ratio of two pairs of corresponding sides equal:
$\frac{PQ}{TQ} = \frac{QS}{QR}$
Consider the angle included between these sides in both triangles.
In $\triangle PQS$, the angle included between sides PQ and QS is $\angle PQS$.
In $\triangle TQR$, the angle included between sides TQ and QR is $\angle TQR$.
From the figure, we can see that $\angle PQS$ and $\angle TQR$ represent the same angle, which is $\angle 1$.
$\angle PQS = \angle TQR = \angle 1$
[Common angle]
We have shown that the ratio of two pairs of corresponding sides is equal, and the included angle between these sides is also equal.
Therefore, by the SAS (Side-Angle-Side) similarity criterion:
$\triangle PQS \sim \triangle TQR$
Hence Proved.
Question 5. S and T are points on sides PR and QR of ∆ PQR such that ∠P = ∠RTS. Show that ∆ RPQ ~ ∆ RTS.
Answer:
Given:
In $\triangle PQR$:
S is a point on side PR.
T is a point on side QR.
$\angle P = \angle RTS$
(Given condition)
(Here $\angle P$ means $\angle QPR$ or $\angle RPQ$)
To Prove:
$\triangle RPQ \sim \triangle RTS$
Proof:
We need to compare the triangles $\triangle RPQ$ and $\triangle RTS$.
In $\triangle RPQ$ and $\triangle RTS$:
We are given that:
$\angle RPQ = \angle RTS$
[Given, where $\angle P = \angle RPQ$]
Now consider the angle at vertex R.
$\angle PRQ$ is an angle in $\triangle RPQ$.
$\angle SRT$ is an angle in $\triangle RTS$.
These two angles represent the same angle $\angle R$.
$\angle PRQ = \angle SRT$
[Common angle $\angle R$]
So, in $\triangle RPQ$ and $\triangle RTS$, two pairs of corresponding angles are equal:
$\angle RPQ = \angle RTS$
$\angle PRQ = \angle SRT$
Therefore, by the AA (Angle-Angle) similarity criterion, the two triangles are similar.
The correspondence is $R \leftrightarrow R$, $P \leftrightarrow T$, $Q \leftrightarrow S$.
$\triangle RPQ \sim \triangle RTS$
Hence Proved.
Question 6. In Fig. 6.37, if ∆ ABE ≅ ∆ ACD, show that ∆ ADE ~ ∆ ABC.
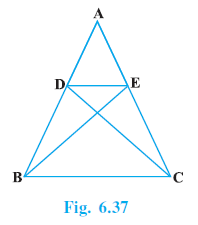
Answer:
Given:
In the figure, we are given that triangle ABE is congruent to triangle ACD:
$\triangle ABE \cong \triangle ACD$
(Given Congruence)
To Prove:
Triangle ADE is similar to triangle ABC:
$\triangle ADE \sim \triangle ABC$
Proof:
Since $\triangle ABE \cong \triangle ACD$, their corresponding parts are equal (CPCT - Corresponding Parts of Congruent Triangles).
Therefore, we have:
$AB = AC$
[CPCT] ... (i)
$AE = AD$
[CPCT]
We can rewrite the second equality as:
$AD = AE$
... (ii)
Also from CPCT, the corresponding angles are equal:
$\angle BAE = \angle CAD$
[CPCT]
Let's consider the angle $\angle DAE$. From the figure, $\angle DAE = \angle CAD$. Therefore, $\angle DAE = \angle BAE$. This represents the common angle $\angle A$ for both triangles $\triangle ADE$ and $\triangle ABC$.
$\angle DAE = \angle BAC$
[Common angle $\angle A$] ... (iii)
Now, let's examine the ratios of the sides that include this common angle in triangles $\triangle ADE$ and $\triangle ABC$. We need to check if $\frac{AD}{AB} = \frac{AE}{AC}$.
From equation (i), we have $AB = AC$.
From equation (ii), we have $AD = AE$.
Divide equation (ii) by equation (i):
$\frac{AD}{AB} = \frac{AE}{AC}$
... (iv)
(This is valid because if $x=y$ and $p=q$, then $\frac{x}{p} = \frac{y}{q}$, assuming $p, q \neq 0$).
Now, consider $\triangle ADE$ and $\triangle ABC$.
From (iii), we have $\angle DAE = \angle BAC$ (Angle).
From (iv), we have $\frac{AD}{AB} = \frac{AE}{AC}$ (Ratio of including sides).
Therefore, by the SAS (Side-Angle-Side) similarity criterion, the two triangles are similar.
$\triangle ADE \sim \triangle ABC$
Hence Proved.
Question 7. In Fig. 6.38, altitudes AD and CE of ∆ ABC intersect each other at the point P. Show that:
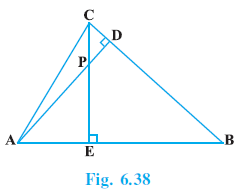
(i) ∆AEP ~ ∆CDP
(ii) ∆ABD ~ ∆CBE
(iii) ∆AEP ~ ∆ADB
(iv) ∆ PDC ~ ∆BEC
Answer:
Given:
In $\triangle ABC$:
AD is an altitude, so $AD \perp BC$. This implies $\angle ADB = 90^\circ$ and $\angle ADC = 90^\circ$.
CE is an altitude, so $CE \perp AB$. This implies $\angle CEB = 90^\circ$ and $\angle CEA = 90^\circ$.
Altitudes AD and CE intersect at point P.
To Prove:
(i) $\triangle AEP \sim \triangle CDP$
(ii) $\triangle ABD \sim \triangle CBE$
(iii) $\triangle AEP \sim \triangle ADB$
(iv) $\triangle PDC \sim \triangle BEC$
Proof:
(i) Proof of $\triangle AEP \sim \triangle CDP$
Consider $\triangle AEP$ and $\triangle CDP$.
$\angle AEP = 90^\circ$
[Since $CE \perp AB$]
$\angle CDP = 90^\circ$
[Since $AD \perp BC$]
Therefore, $\angle AEP = \angle CDP = 90^\circ$.
Also, the angles at the intersection P:
$\angle APE = \angle CPD$
[Vertically opposite angles]
Since two pairs of corresponding angles are equal, the triangles are similar by the AA similarity criterion.
$\triangle AEP \sim \triangle CDP$.
(ii) Proof of $\triangle ABD \sim \triangle CBE$
Consider $\triangle ABD$ and $\triangle CBE$.
$\angle ADB = 90^\circ$
[Since $AD \perp BC$]
$\angle CEB = 90^\circ$
[Since $CE \perp AB$]
Therefore, $\angle ADB = \angle CEB = 90^\circ$.
Now consider angle B:
$\angle ABD = \angle CBE$
[Common angle $\angle B$]
Since two pairs of corresponding angles are equal, the triangles are similar by the AA similarity criterion.
$\triangle ABD \sim \triangle CBE$.
(iii) Proof of $\triangle AEP \sim \triangle ADB$
Consider $\triangle AEP$ and $\triangle ADB$.
$\angle AEP = 90^\circ$
[Since $CE \perp AB$]
$\angle ADB = 90^\circ$
[Since $AD \perp BC$]
Therefore, $\angle AEP = \angle ADB = 90^\circ$.
Now consider angle A:
$\angle PAE = \angle DAB$
[Common angle $\angle A$]
Since two pairs of corresponding angles are equal, the triangles are similar by the AA similarity criterion.
$\triangle AEP \sim \triangle ADB$.
(iv) Proof of $\triangle PDC \sim \triangle BEC$
Consider $\triangle PDC$ and $\triangle BEC$.
$\angle PDC = 90^\circ$
[Since $AD \perp BC$]
$\angle BEC = 90^\circ$
[Since $CE \perp AB$]
Therefore, $\angle PDC = \angle BEC = 90^\circ$.
Now consider angle C:
$\angle PCD = \angle BCE$
[Common angle $\angle C$]
Since two pairs of corresponding angles are equal, the triangles are similar by the AA similarity criterion.
$\triangle PDC \sim \triangle BEC$.
Question 8. E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ∆ ABE ~ ∆ CFB.
Answer:
Given:
ABCD is a parallelogram.
E is a point on the side AD produced.
The line segment BE intersects the side CD at point F.
To Prove:
$\triangle ABE \sim \triangle CFB$
Proof:
We need to compare the angles of $\triangle ABE$ and $\triangle CFB$.
Since ABCD is a parallelogram, we know its properties:
1. Opposite sides are parallel: $AB \parallel DC$ and $AD \parallel BC$.
2. Opposite angles are equal: $\angle DAB = \angle BCD$ and $\angle ABC = \angle ADC$.
Consider $\triangle ABE$ and $\triangle CFB$:
Comparing $\angle BAE$ and $\angle FCB$:
$\angle BAE = \angle FCB$
[Opposite angles of parallelogram ABCD are equal, $\angle A = \angle C$]
Now, consider the parallel lines formed by extending AD and BC.
Since $AD \parallel BC$ (opposite sides of parallelogram), the line segment AE (which is AD produced) is also parallel to BC.
$AE \parallel BC$
Consider the line BE as a transversal intersecting the parallel lines AE and BC.
The alternate interior angles formed must be equal.
$\angle AEB = \angle CBF$
[Alternate interior angles, since $AE \parallel BC$ and BE is transversal]
So, in $\triangle ABE$ and $\triangle CFB$, we have found two pairs of corresponding angles that are equal:
$\angle BAE = \angle FCB$
$\angle AEB = \angle CBF$
Therefore, by the AA (Angle-Angle) similarity criterion, the two triangles are similar.
$\triangle ABE \sim \triangle CFB$
Hence Proved.
(Note: We could also use the third pair of angles. Since $AB \parallel DC$, considering BE as transversal, $\angle ABE$ and $\angle BFC$ are not directly related in a standard way. However, since $\triangle ABE \sim \triangle CFB$ by AA, the third pair of angles must also be equal: $\angle ABE = \angle BFC$. This equality can also be proved independently using exterior angle properties related to parallel lines if needed, but AA is sufficient.)
Question 9. In Fig. 6.39, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that:
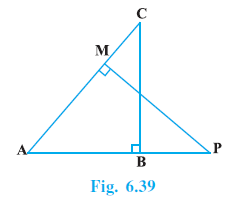
(i) ∆ABC ~ ∆AMP
(ii) $\frac{CA}{PA}$ = $\frac{BC}{MP}$
Answer:
Given:
ABC and AMP are two right triangles.
$\triangle ABC$ is right-angled at B ($\angle ABC = 90^\circ$).
$\triangle AMP$ is right-angled at M ($\angle AMP = 90^\circ$).
To Prove:
(i) $\triangle ABC \sim \triangle AMP$
(ii) $\frac{CA}{PA} = \frac{BC}{MP}$
Proof:
(i) Proof of $\triangle ABC \sim \triangle AMP$
Consider the triangles $\triangle ABC$ and $\triangle AMP$.
We are given the right angles:
$\angle ABC = 90^\circ$
[Given]
$\angle AMP = 90^\circ$
[Given]
Therefore, $\angle ABC = \angle AMP$.
Now consider the angle at vertex A.
$\angle CAB$ is an angle in $\triangle ABC$.
$\angle MAP$ is an angle in $\triangle AMP$.
These two represent the same angle.
$\angle CAB = \angle MAP$
[Common angle $\angle A$]
Since two pairs of corresponding angles in $\triangle ABC$ and $\triangle AMP$ are equal, the triangles are similar by the AA (Angle-Angle) similarity criterion.
The correspondence is $A \leftrightarrow A$, $B \leftrightarrow M$, $C \leftrightarrow P$.
Thus, $\triangle ABC \sim \triangle AMP$.
Hence Proved (i).
(ii) Proof of $\frac{CA}{PA} = \frac{BC}{MP}$
From part (i), we have proved that $\triangle ABC \sim \triangle AMP$.
Since the triangles are similar, the ratio of their corresponding sides must be equal.
Based on the correspondence $A \leftrightarrow A$, $B \leftrightarrow M$, $C \leftrightarrow P$, the corresponding sides are:
AB corresponds to AM
BC corresponds to MP
CA corresponds to PA
Therefore, the ratio of corresponding sides is:
$\frac{AB}{AM} = \frac{BC}{MP} = \frac{CA}{PA}$
[Ratio of corresponding sides of similar triangles]
From this equality, we can select the required ratio involving CA, PA, BC, and MP:
$\frac{BC}{MP} = \frac{CA}{PA}$
Rearranging to match the required format:
$\frac{CA}{PA} = \frac{BC}{MP}$
Hence Proved (ii).
Question 10. CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ∆ ABC and ∆ EFG respectively. If ∆ABC ~ ∆ FEG, show that:
(i) $\frac{CD}{GH}$ = $\frac{AC}{FG}$
(ii) ∆ DCB ~ ∆ HGE
(iii) ∆ DCA ~ ∆ HGF
Answer:
Given:
$\triangle ABC \sim \triangle FEG$.
CD is the bisector of $\angle ACB$, with D on AB.
GH is the bisector of $\angle FGE$, with H on FE.
To Prove:
(i) $\frac{CD}{GH} = \frac{AC}{FG}$
(ii) $\triangle DCB \sim \triangle HGE$
(iii) $\triangle DCA \sim \triangle HGF$
Proof:
Since $\triangle ABC \sim \triangle FEG$, we know that their corresponding angles are equal and the ratios of their corresponding sides are equal.
Corresponding Angles:
$\angle A = \angle F$
... (a)
$\angle B = \angle E$
... (b)
$\angle ACB = \angle FGE$
... (c)
Ratio of Corresponding Sides:
$\frac{AB}{FE} = \frac{BC}{EG} = \frac{AC}{FG}$
... (d)
Since CD bisects $\angle ACB$ and GH bisects $\angle FGE$:
$\angle ACD = \angle BCD = \frac{1}{2} \angle ACB$
... (e)
$\angle FGH = \angle EGH = \frac{1}{2} \angle FGE$
... (f)
From (c), $\angle ACB = \angle FGE$. Therefore, half of these angles are also equal:
$\frac{1}{2} \angle ACB = \frac{1}{2} \angle FGE$
This implies:
$\angle ACD = \angle FGH$
... (g)
$\angle BCD = \angle EGH$
... (h)
(iii) Proof of $\triangle DCA \sim \triangle HGF$
Consider $\triangle DCA$ and $\triangle HGF$.
From (a):
$\angle DAC = \angle HFG$
($\angle A = \angle F$)
From (g):
$\angle ACD = \angle FGH$
Since two pairs of corresponding angles are equal, by the AA similarity criterion:
$\triangle DCA \sim \triangle HGF$.
Hence Proved (iii).
(i) Proof of $\frac{CD}{GH} = \frac{AC}{FG}$
From part (iii), we proved that $\triangle DCA \sim \triangle HGF$.
Since the triangles are similar, the ratio of their corresponding sides is equal.
The correspondence is $D \leftrightarrow H$, $C \leftrightarrow G$, $A \leftrightarrow F$.
Therefore:
$\frac{DC}{HG} = \frac{CA}{GF} = \frac{AD}{FH}$
Considering the first two parts of the equality and writing the side names consistently:
$\frac{CD}{GH} = \frac{AC}{FG}$.
Hence Proved (i).
(ii) Proof of $\triangle DCB \sim \triangle HGE$
Consider $\triangle DCB$ and $\triangle HGE$.
From (b):
$\angle DBC = \angle HEG$
($\angle B = \angle E$)
From (h):
$\angle BCD = \angle EGH$
Since two pairs of corresponding angles are equal, by the AA similarity criterion:
$\triangle DCB \sim \triangle HGE$.
Hence Proved (ii).
Question 11. In Fig. 6.40, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD⊥BC and EF⊥AC, prove that ∆ ABD ~ ∆ ECF.

Answer:
Given:
$\triangle ABC$ is an isosceles triangle with $AB = AC$.
E is a point on side CB produced.
$AD \perp BC$, which implies $\angle ADB = 90^\circ$.
$EF \perp AC$, which implies $\angle EFC = 90^\circ$.
To Prove:
$\triangle ABD \sim \triangle ECF$
Proof:
Since $\triangle ABC$ is an isosceles triangle with $AB = AC$, the angles opposite to these equal sides must be equal.
$\angle ABC = \angle ACB$
[Angles opposite to equal sides of a triangle are equal]
We can write $\angle ABC$ as $\angle ABD$ (as D lies on BC) and $\angle ACB$ as $\angle ECF$ (as E lies on CB produced).
$\angle ABD = \angle ECF$
... (i)
Now, consider the triangles $\triangle ABD$ and $\triangle ECF$.
From the given information about altitudes:
$\angle ADB = 90^\circ$
[Given $AD \perp BC$]
$\angle EFC = 90^\circ$
[Given $EF \perp AC$]
Therefore,
$\angle ADB = \angle EFC = 90^\circ$
... (ii)
From equation (i) and equation (ii), we have two pairs of corresponding angles equal in $\triangle ABD$ and $\triangle ECF$:
$\angle ABD = \angle ECF$
$\angle ADB = \angle EFC$
Therefore, by the AA (Angle-Angle) similarity criterion, the two triangles are similar.
$\triangle ABD \sim \triangle ECF$
Hence Proved.
Question 12. Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ∆ PQR (see Fig. 6.41). Show that ∆ ABC ~ ∆ PQR.
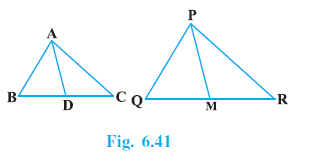
Answer:
Given:
Two triangles $\triangle ABC$ and $\triangle PQR$.
AD is the median to side BC in $\triangle ABC$, so D is the midpoint of BC ($BD = DC = \frac{1}{2}BC$).
PM is the median to side QR in $\triangle PQR$, so M is the midpoint of QR ($QM = MR = \frac{1}{2}QR$).
The sides AB, BC and median AD of $\triangle ABC$ are respectively proportional to sides PQ, QR and median PM of $\triangle PQR$.
$\frac{AB}{PQ} = \frac{BC}{QR} = \frac{AD}{PM}$
... (i)
To Prove:
$\triangle ABC \sim \triangle PQR$.
Proof:
From the given proportionality (i), we have:
$\frac{AB}{PQ} = \frac{BC}{QR} = \frac{AD}{PM}$
Since D is the midpoint of BC, $BC = 2BD$.
Since M is the midpoint of QR, $QR = 2QM$.
Substitute these into the second ratio of the given proportionality:
$\frac{BC}{QR} = \frac{2BD}{2QM} = \frac{BD}{QM}$
Now, substitute this back into the proportionality (i):
$\frac{AB}{PQ} = \frac{BD}{QM} = \frac{AD}{PM}$
... (ii)
Consider the triangles $\triangle ABD$ and $\triangle PQM$.
From equation (ii), we have:
$\frac{AB}{PQ} = \frac{BD}{QM} = \frac{AD}{PM}$
This shows that all three pairs of corresponding sides of $\triangle ABD$ and $\triangle PQM$ are proportional.
Therefore, by the SSS (Side-Side-Side) similarity criterion:
$\triangle ABD \sim \triangle PQM$.
Since the triangles $\triangle ABD$ and $\triangle PQM$ are similar, their corresponding angles must be equal.
$\angle ABD = \angle PQM$
[Corresponding angles of similar triangles]
This means $\angle B = \angle Q$.
$\angle B = \angle Q$
... (iii)
Now consider the original triangles $\triangle ABC$ and $\triangle PQR$.
From the given proportionality (i), we have:
$\frac{AB}{PQ} = \frac{BC}{QR}$
[Ratio of two sides]
From (iii), we have the included angles equal:
$\angle B = \angle Q$
[Included angle]
Therefore, by the SAS (Side-Angle-Side) similarity criterion:
$\triangle ABC \sim \triangle PQR$.
Hence Proved.
Question 13. D is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC. Show that CA2 = CB.CD.
Answer:
Given:
A triangle $\triangle ABC$.
D is a point on the side BC.
$\angle ADC = \angle BAC$
(Given condition)
To Prove:
$CA^2 = CB \cdot CD$
Proof:
To prove the relationship involving the sides, we should look for similar triangles that include these sides.
Consider the triangles $\triangle ABC$ and $\triangle DAC$.
In $\triangle ABC$ and $\triangle DAC$:
We are given:
$\angle BAC = \angle ADC$
[Given]
Now consider the angle at vertex C:
$\angle ACB$ is an angle in $\triangle ABC$.
$\angle DCA$ is an angle in $\triangle DAC$.
These represent the same angle.
$\angle ACB = \angle DCA$
[Common angle $\angle C$]
Since two pairs of corresponding angles in $\triangle ABC$ and $\triangle DAC$ are equal, the triangles are similar by the AA (Angle-Angle) similarity criterion.
The correspondence of vertices is $A \leftrightarrow D$, $B \leftrightarrow A$, $C \leftrightarrow C$. (Note: Angle A of ABC corresponds to Angle D of DAC, Angle C of ABC corresponds to Angle C of DAC, so Angle B of ABC must correspond to Angle A of DAC).
Therefore, $\triangle ABC \sim \triangle DAC$.
Since the triangles are similar, the ratio of their corresponding sides must be equal.
$\frac{AB}{DA} = \frac{BC}{AC} = \frac{AC}{DC}$
[Ratio of corresponding sides of similar triangles]
Consider the second and third parts of this proportion:
$\frac{BC}{AC} = \frac{AC}{DC}$
Rewriting using the notation CA, CB, CD:
$\frac{CB}{CA} = \frac{CA}{CD}$
Cross-multiplying the terms:
$CB \cdot CD = CA \cdot CA$
$CA^2 = CB \cdot CD$
Hence Proved.
Question 14. Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ∆ABC ~ ∆ PQR.
Answer:
Given:
Two triangles $\triangle ABC$ and $\triangle PQR$.
AD is the median to side BC in $\triangle ABC$ (D is the midpoint of BC).
PM is the median to side QR in $\triangle PQR$ (M is the midpoint of QR).
The sides AB, AC and median AD of $\triangle ABC$ are respectively proportional to sides PQ, PR and median PM of $\triangle PQR$.
$\frac{AB}{PQ} = \frac{AC}{PR} = \frac{AD}{PM}$
... (i)
To Prove:
$\triangle ABC \sim \triangle PQR$.
Construction Required:
Produce AD to E such that AD = DE. Join CE.
Produce PM to N such that PM = MN. Join RN.
Proof:
Consider $\triangle ABD$ and $\triangle ECD$.
AD = ED
(By Construction)
BD = CD
(AD is the median to BC)
$\angle ADB = \angle EDC$
(Vertically opposite angles)
Therefore, by SAS congruence criterion:
$\triangle ABD \cong \triangle ECD$.
By CPCT (Corresponding Parts of Congruent Triangles):
$AB = EC$
... (ii)
Similarly, consider $\triangle PQM$ and $\triangle NRM$.
PM = NM
(By Construction)
QM = RM
(PM is the median to QR)
$\angle PMQ = \angle NMR$
(Vertically opposite angles)
Therefore, by SAS congruence criterion:
$\triangle PQM \cong \triangle NRM$.
By CPCT:
$PQ = NR$
... (iii)
Now, take the given proportionality from (i):
$\frac{AB}{PQ} = \frac{AC}{PR} = \frac{AD}{PM}$
Substitute $AB = EC$ from (ii) and $PQ = NR$ from (iii):
$\frac{EC}{NR} = \frac{AC}{PR} = \frac{AD}{PM}$
Also, by construction $AE = AD + DE = AD + AD = 2AD$, so $AD = \frac{1}{2}AE$.
And $PN = PM + MN = PM + PM = 2PM$, so $PM = \frac{1}{2}PN$.
Substitute these into the third ratio:
$\frac{AD}{PM} = \frac{\frac{1}{2}AE}{\frac{1}{2}PN} = \frac{AE}{PN}$
So the proportionality becomes:
$\frac{EC}{NR} = \frac{AC}{PR} = \frac{AE}{PN}$
... (iv)
Consider $\triangle ACE$ and $\triangle PRN$.
From (iv), we have $\frac{AC}{PR} = \frac{CE}{RN} = \frac{AE}{PN}$.
Since all three pairs of corresponding sides are proportional, by the SSS similarity criterion:
$\triangle ACE \sim \triangle PRN$.
Therefore, corresponding angles are equal:
$\angle CAE = \angle RPN$
[Corresponding angles of similar triangles] ... (v)
Similarly, from $\triangle ABD \cong \triangle ECD$, we get $\angle BAD = \angle CED$.
From $\triangle PQM \cong \triangle NRM$, we get $\angle QPM = \angle RNM$.
Let's revisit the similarity $\triangle ACE \sim \triangle PRN$. The angles are $\angle CAE = \angle RPN$, $\angle ACE = \angle PRN$, $\angle AEC = \angle PNR$.
Consider the original congruence $\triangle ABD \cong \triangle ECD$. This gives $\angle BAD = \angle CED (\angle AEC)$.
Consider the original congruence $\triangle PQM \cong \triangle NRM$. This gives $\angle QPM = \angle RNM (\angle PNR)$.
Since $\angle AEC = \angle PNR$ (from $\triangle ACE \sim \triangle PRN$), and $\angle BAD = \angle AEC$, and $\angle QPM = \angle PNR$, we get:
$\angle BAD = \angle QPM$
... (vi)
Adding equations (v) and (vi):
$\angle CAE + \angle BAD = \angle RPN + \angle QPM$
From the figure, $\angle CAE + \angle BAD = \angle BAC$.
From the figure, $\angle RPN + \angle QPM = \angle QPR$.
Therefore,
$\angle BAC = \angle QPR$
... (vii)
Now, consider the triangles $\triangle ABC$ and $\triangle PQR$.
From the given information (i), we have:
$\frac{AB}{PQ} = \frac{AC}{PR}$
From equation (vii), we have the included angle:
$\angle BAC = \angle QPR$
Therefore, by the SAS (Side-Angle-Side) similarity criterion:
$\triangle ABC \sim \triangle PQR$.
Hence Proved.
Question 15. A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
Answer:
Given:
Height of the vertical pole = 6 m.
Length of the shadow of the pole = 4 m.
Length of the shadow of the tower = 28 m.
Both shadows are cast at the same time.
To Find:
The height of the tower.
Solution:
Let AB be the vertical pole and BC be its shadow. Let PQ be the tower and QR be its shadow.
Height of pole, $AB = 6$ m.
Length of pole's shadow, $BC = 4$ m.
Length of tower's shadow, $QR = 28$ m.
Let the height of the tower be $PQ = H$ meters.
At the same time, the angle of elevation of the sun is the same for both the pole and the tower. This means the angle formed by the top of the object, the tip of the shadow, and the base of the object on the ground is the same.
Consider $\triangle ABC$ formed by the pole and its shadow, and $\triangle PQR$ formed by the tower and its shadow.
Both the pole and the tower stand vertically on the ground.
$\angle ABC = 90^\circ$
[Pole is vertical]
$\angle PQR = 90^\circ$
[Tower is vertical]
Therefore, $\angle ABC = \angle PQR$.
The angle of elevation of the sun at the same time is the same for both triangles:
$\angle ACB = \angle PRQ$
[Same angle of elevation]
Since two pairs of corresponding angles are equal, by the AA (Angle-Angle) similarity criterion:
$\triangle ABC \sim \triangle PQR$
Since the triangles are similar, the ratio of their corresponding sides is equal:
$\frac{AB}{PQ} = \frac{BC}{QR}$
[Ratio of corresponding sides of similar triangles]
Substitute the known values:
$\frac{6}{H} = \frac{4}{28}$
Now, solve for H:
$4 \times H = 6 \times 28$
$H = \frac{6 \times 28}{4}$
$H = \frac{6 \times \cancel{28}^7}{\cancel{4}_1}$
$H = 6 \times 7$
$H = 42$
Thus, the height of the tower is 42 meters.
Question 16. If AD and PM are medians of triangles ABC and PQR, respectively where ∆ ABC ~ ∆ PQR, prove that $\frac{AB}{PQ}$ = $\frac{AD}{PM}$ .
Answer:
Given:
$\triangle ABC \sim \triangle PQR$.
AD is the median of $\triangle ABC$ to side BC (D is the midpoint of BC).
PM is the median of $\triangle PQR$ to side QR (M is the midpoint of QR).
To Prove:
$\frac{AB}{PQ} = \frac{AD}{PM}$.
Proof:
Since $\triangle ABC \sim \triangle PQR$, we know that their corresponding angles are equal and the ratios of their corresponding sides are equal.
Corresponding Angles:
$\angle A = \angle P$, $\angle B = \angle Q$, $\angle C = \angle R$
... (i)
Ratio of Corresponding Sides:
$\frac{AB}{PQ} = \frac{BC}{QR} = \frac{AC}{PR}$
... (ii)
Since AD is the median to BC, $D$ is the midpoint of BC.
$BD = DC = \frac{1}{2}BC$, or $BC = 2BD$.
Since PM is the median to QR, $M$ is the midpoint of QR.
$QM = MR = \frac{1}{2}QR$, or $QR = 2QM$.
From the ratio in (ii), consider:
$\frac{AB}{PQ} = \frac{BC}{QR}$
Substitute $BC = 2BD$ and $QR = 2QM$:
$\frac{AB}{PQ} = \frac{2BD}{2QM}$
$\frac{AB}{PQ} = \frac{BD}{QM}$
... (iii)
Now, consider the triangles $\triangle ABD$ and $\triangle PQM$.
From (i), we have:
$\angle B = \angle Q$
($\angle ABD = \angle PQM$)
From (iii), we have the ratio of the sides including these angles:
$\frac{AB}{PQ} = \frac{BD}{QM}$
Therefore, by the SAS (Side-Angle-Side) similarity criterion:
$\triangle ABD \sim \triangle PQM$.
Since the triangles $\triangle ABD$ and $\triangle PQM$ are similar, the ratio of their corresponding sides is equal.
The corresponding sides are AB to PQ, BD to QM, and AD to PM.
$\frac{AB}{PQ} = \frac{BD}{QM} = \frac{AD}{PM}$
[Ratio of corresponding sides of similar triangles]
From this equality, we can extract the required result:
$\frac{AB}{PQ} = \frac{AD}{PM}$
Hence Proved.
Example 9 (Before Exercise 6.4)
Example 9. In Fig. 6.43, the line segment XY is parallel to side AC of ∆ ABC and it divides the triangle into two parts of equal areas. Find the ratio $\frac{AX}{AB}$ .
Answer:
Given:
In $\triangle ABC$, the line segment XY is parallel to side AC ($XY \parallel AC$).
X is a point on AB and Y is a point on BC.
The line segment XY divides $\triangle ABC$ into two parts of equal areas.
This means, area($\triangle XBY$) = area(trapezium AXYC).
To Find:
The ratio $\frac{AX}{AB}$.
Solution:
We are given that $XY \parallel AC$.
Consider $\triangle XBY$ and $\triangle ABC$.
$\angle BXY = \angle BAC$
[Corresponding angles, as $XY \parallel AC$ and AB is transversal]
$\angle BYX = \angle BCA$
[Corresponding angles, as $XY \parallel AC$ and BC is transversal]
$\angle XBY = \angle ABC$
[Common angle B]
Therefore, by AAA similarity criterion (or AA similarity), the triangles are similar:
$\triangle XBY \sim \triangle ABC$.
We know that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
$\frac{\text{area}(\triangle XBY)}{\text{area}(\triangle ABC)} = \left(\frac{XB}{AB}\right)^2 = \left(\frac{BY}{BC}\right)^2 = \left(\frac{XY}{AC}\right)^2$
... (i)
We are given that XY divides the triangle into two parts of equal areas:
area($\triangle XBY$) = area(trapezium AXYC)
The total area of $\triangle ABC$ is the sum of these two areas:
area($\triangle ABC$) = area($\triangle XBY$) + area(trapezium AXYC)
area($\triangle ABC$) = area($\triangle XBY$) + area($\triangle XBY$)
area($\triangle ABC$) = 2 $\times$ area($\triangle XBY$)
Therefore, the ratio of the areas is:
$\frac{\text{area}(\triangle XBY)}{\text{area}(\triangle ABC)} = \frac{1}{2}$
... (ii)
Equating the results from (i) and (ii):
$\left(\frac{XB}{AB}\right)^2 = \frac{1}{2}$
Taking the square root on both sides (lengths are positive):
$\frac{XB}{AB} = \frac{1}{\sqrt{2}}$
Rationalizing the denominator:
$\frac{XB}{AB} = \frac{1 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}} = \frac{\sqrt{2}}{2}$
... (iii)
We need to find the ratio $\frac{AX}{AB}$.
From the figure, we can see that $AX = AB - XB$.
Divide by AB:
$\frac{AX}{AB} = \frac{AB - XB}{AB}$
$\frac{AX}{AB} = \frac{AB}{AB} - \frac{XB}{AB}$
$\frac{AX}{AB} = 1 - \frac{XB}{AB}$
Substitute the value of $\frac{XB}{AB}$ from (iii):
$\frac{AX}{AB} = 1 - \frac{\sqrt{2}}{2}$
$\frac{AX}{AB} = \frac{2 - \sqrt{2}}{2}$
Therefore, the required ratio is $\frac{AX}{AB} = \frac{2 - \sqrt{2}}{2}$.
Exercise 6.4
Question 1. Let ∆ ABC ~ ∆ DEF and their areas be, respectively, 64 cm2 and 121 cm2 . If EF = 15.4 cm, find BC.
Answer:
Given:
$\triangle ABC \sim \triangle DEF$.
Area($\triangle ABC$) = 64 cm2.
Area($\triangle DEF$) = 121 cm2.
$EF = 15.4$ cm.
To Find:
The length of side BC.
Solution:
We know that if two triangles are similar, then the ratio of their areas is equal to the square of the ratio of their corresponding sides.
Since $\triangle ABC \sim \triangle DEF$, the correspondence of vertices is $A \leftrightarrow D$, $B \leftrightarrow E$, $C \leftrightarrow F$.
Therefore, the corresponding sides are AB and DE, BC and EF, AC and DF.
According to the theorem on areas of similar triangles:
$\frac{\text{Area}(\triangle ABC)}{\text{Area}(\triangle DEF)} = \left(\frac{AB}{DE}\right)^2 = \left(\frac{BC}{EF}\right)^2 = \left(\frac{AC}{DF}\right)^2$
We are given the areas and the length of EF, and we need to find BC. So we use the relation involving BC and EF:
$\frac{\text{Area}(\triangle ABC)}{\text{Area}(\triangle DEF)} = \left(\frac{BC}{EF}\right)^2$
Substitute the given values:
$\frac{64}{121} = \left(\frac{BC}{15.4}\right)^2$
Take the square root of both sides. Since lengths are positive, we take the positive square root:
$\sqrt{\frac{64}{121}} = \sqrt{\left(\frac{BC}{15.4}\right)^2}$
$\frac{\sqrt{64}}{\sqrt{121}} = \frac{BC}{15.4}$
$\frac{8}{11} = \frac{BC}{15.4}$
Now, solve for BC:
$BC = \frac{8}{11} \times 15.4$
$BC = \frac{8 \times 15.4}{11}$
$BC = \frac{8 \times \cancel{15.4}^{1.4}}{\cancel{11}_1}$
$BC = 8 \times 1.4$
$BC = 11.2$
Therefore, the length of side BC is 11.2 cm.
Question 2. Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
Answer:
Given:
ABCD is a trapezium with $AB \parallel DC$.
Diagonals AC and BD intersect at point O.
$AB = 2 CD$
To Find:
The ratio of the areas of $\triangle AOB$ and $\triangle COD$, i.e., $\frac{\text{Area}(\triangle AOB)}{\text{Area}(\triangle COD)}$.
Solution:
Consider the triangles $\triangle AOB$ and $\triangle COD$.
Since $AB \parallel DC$ and AC is a transversal:
$\angle OAB = \angle OCD$
[Alternate interior angles]
Since $AB \parallel DC$ and BD is a transversal:
$\angle OBA = \angle ODC$
[Alternate interior angles]
Also, at the intersection O:
$\angle AOB = \angle COD$
[Vertically opposite angles]
Therefore, by the AAA similarity criterion (or AA similarity), the triangles are similar:
$\triangle AOB \sim \triangle COD$.
We know that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
The corresponding sides are AB and CD, AO and CO, BO and DO.
So, we can write:
$\frac{\text{Area}(\triangle AOB)}{\text{Area}(\triangle COD)} = \left(\frac{AB}{CD}\right)^2$
We are given the relationship $AB = 2 CD$. Substitute this into the equation:
$\frac{\text{Area}(\triangle AOB)}{\text{Area}(\triangle COD)} = \left(\frac{2 CD}{CD}\right)^2$
Simplify the expression:
$\frac{\text{Area}(\triangle AOB)}{\text{Area}(\triangle COD)} = \left(\frac{2 \cancel{CD}}{\cancel{CD}}\right)^2$
$\frac{\text{Area}(\triangle AOB)}{\text{Area}(\triangle COD)} = (2)^2$
$\frac{\text{Area}(\triangle AOB)}{\text{Area}(\triangle COD)} = 4$
The ratio can be written as $\frac{4}{1}$.
Therefore, the ratio of the areas of $\triangle AOB$ to $\triangle COD$ is 4 : 1.
Question 3. In Fig. 6.44, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that
$\frac{ar (ABC)}{ar (DBC)}$ = $\frac{AO}{DO}$.

Answer:
Given:
$\triangle ABC$ and $\triangle DBC$ are two triangles on the same base BC.
The line segment AD intersects the base BC at point O.
To Prove:
$\frac{\text{Area}(\triangle ABC)}{\text{Area}(\triangle DBC)} = \frac{AO}{DO}$
(Using the notation 'ar' for area as in the question: $\frac{ar (ABC)}{ar (DBC)} = \frac{AO}{DO}$)
Construction Required:
Draw altitude AM from vertex A to the base BC ($AM \perp BC$).
Draw altitude DN from vertex D to the base BC ($DN \perp BC$).
Proof:
The area of a triangle is given by the formula: $\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}$.
For $\triangle ABC$, the base is BC and the height is AM.
ar($\triangle ABC$) = $\frac{1}{2} \times BC \times AM$
... (i)
For $\triangle DBC$, the base is BC and the height is DN.
ar($\triangle DBC$) = $\frac{1}{2} \times BC \times DN$
... (ii)
Now, find the ratio of the areas by dividing equation (i) by equation (ii):
$\frac{ar (ABC)}{ar (DBC)} = \frac{\frac{1}{2} \times BC \times AM}{\frac{1}{2} \times BC \times DN}$
The terms $\frac{1}{2}$ and $BC$ cancel out:
$\frac{ar (ABC)}{ar (DBC)} = \frac{AM}{DN}$
... (iii)
Now, consider the triangles $\triangle AMO$ and $\triangle DNO$.
By construction:
$\angle AMO = 90^\circ$
[Since $AM \perp BC$]
$\angle DNO = 90^\circ$
[Since $DN \perp BC$]
Therefore, $\angle AMO = \angle DNO$.
Also, the angles at the intersection O:
$\angle AOM = \angle DON$
[Vertically opposite angles]
Since two pairs of corresponding angles in $\triangle AMO$ and $\triangle DNO$ are equal, the triangles are similar by the AA similarity criterion.
$\triangle AMO \sim \triangle DNO$.
Since the triangles are similar, the ratio of their corresponding sides is equal.
The correspondence is $A \leftrightarrow D$, $M \leftrightarrow N$, $O \leftrightarrow O$.
$\frac{AM}{DN} = \frac{MO}{NO} = \frac{AO}{DO}$
[Ratio of corresponding sides of similar triangles]
From this, we have:
$\frac{AM}{DN} = \frac{AO}{DO}$
... (iv)
Now, substitute the result from equation (iv) into equation (iii):
$\frac{ar (ABC)}{ar (DBC)} = \frac{AO}{DO}$
Hence Proved.
Question 4. If the areas of two similar triangles are equal, prove that they are congruent.
Answer:
Given:
Two triangles, let's call them $\triangle ABC$ and $\triangle PQR$.
The triangles are similar: $\triangle ABC \sim \triangle PQR$.
The areas of the triangles are equal: Area($\triangle ABC$) = Area($\triangle PQR$).
To Prove:
The triangles are congruent: $\triangle ABC \cong \triangle PQR$.
Proof:
Since $\triangle ABC \sim \triangle PQR$, we know from the theorem on areas of similar triangles that the ratio of their areas is equal to the square of the ratio of their corresponding sides.
$\frac{\text{Area}(\triangle ABC)}{\text{Area}(\triangle PQR)} = \left(\frac{AB}{PQ}\right)^2 = \left(\frac{BC}{QR}\right)^2 = \left(\frac{AC}{PR}\right)^2$
... (i)
We are given that the areas are equal:
Area($\triangle ABC$) = Area($\triangle PQR$)
Dividing both sides by Area($\triangle PQR$) (assuming the area is non-zero):
$\frac{\text{Area}(\triangle ABC)}{\text{Area}(\triangle PQR)} = 1$
... (ii)
From equation (i) and equation (ii), we get:
$1 = \left(\frac{AB}{PQ}\right)^2 = \left(\frac{BC}{QR}\right)^2 = \left(\frac{AC}{PR}\right)^2$
Considering each part separately:
$\left(\frac{AB}{PQ}\right)^2 = 1 \implies \frac{AB}{PQ} = 1$ (Since side lengths are positive)
$\implies AB = PQ$
Similarly,
$\left(\frac{BC}{QR}\right)^2 = 1 \implies \frac{BC}{QR} = 1 \implies BC = QR$
And,
$\left(\frac{AC}{PR}\right)^2 = 1 \implies \frac{AC}{PR} = 1 \implies AC = PR$
Now, consider the triangles $\triangle ABC$ and $\triangle PQR$. We have shown that all three pairs of corresponding sides are equal:
AB = PQ
(Side)
BC = QR
(Side)
AC = PR
(Side)
By the SSS (Side-Side-Side) congruence criterion, if the three sides of one triangle are equal to the three corresponding sides of another triangle, then the two triangles are congruent.
Therefore, $\triangle ABC \cong \triangle PQR$.
Hence Proved.
Question 5. D, E and F are respectively the mid-points of sides AB, BC and CA of ∆ ABC. Find the ratio of the areas of ∆ DEF and ∆ ABC.
Answer:
Given:
In $\triangle ABC$, D, E, and F are the mid-points of sides AB, BC, and CA respectively.
To Find:
The ratio $\frac{\text{Area}(\triangle DEF)}{\text{Area}(\triangle ABC)}$.
Solution:
We will use the Mid-point Theorem, which states that the line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is half of it.
Consider the sides of $\triangle DEF$ formed by joining the mid-points:
Since D and E are mid-points of AB and BC respectively:
$DE \parallel AC$ and $DE = \frac{1}{2}AC$
[By Mid-point Theorem]
Since E and F are mid-points of BC and CA respectively:
$EF \parallel AB$ and $EF = \frac{1}{2}AB$
[By Mid-point Theorem]
Since F and D are mid-points of CA and AB respectively:
$FD \parallel BC$ and $FD = \frac{1}{2}BC$
[By Mid-point Theorem]
Now, consider the triangles $\triangle DEF$ and $\triangle CAB$ (which is the same as $\triangle ABC$).
Let's look at the ratios of the sides:
$\frac{DE}{CA} = \frac{\frac{1}{2}AC}{AC} = \frac{1}{2}$
$\frac{EF}{AB} = \frac{\frac{1}{2}AB}{AB} = \frac{1}{2}$
$\frac{FD}{BC} = \frac{\frac{1}{2}BC}{BC} = \frac{1}{2}$
Since the ratios of the corresponding sides of $\triangle DEF$ and $\triangle CAB$ are equal:
$\frac{DE}{CA} = \frac{EF}{AB} = \frac{FD}{BC} = \frac{1}{2}$
By the SSS (Side-Side-Side) similarity criterion, the two triangles are similar:
$\triangle DEF \sim \triangle CAB$.
According to the theorem on the areas of similar triangles, the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
$\frac{\text{Area}(\triangle DEF)}{\text{Area}(\triangle CAB)} = \left(\frac{DE}{CA}\right)^2 = \left(\frac{EF}{AB}\right)^2 = \left(\frac{FD}{BC}\right)^2$
Using any of these ratios, we get:
$\frac{\text{Area}(\triangle DEF)}{\text{Area}(\triangle CAB)} = \left(\frac{1}{2}\right)^2$
$\frac{\text{Area}(\triangle DEF)}{\text{Area}(\triangle CAB)} = \frac{1}{4}$
Since Area($\triangle CAB$) is the same as Area($\triangle ABC$):
$\frac{\text{Area}(\triangle DEF)}{\text{Area}(\triangle ABC)} = \frac{1}{4}$
Therefore, the ratio of the areas of $\triangle DEF$ and $\triangle ABC$ is 1 : 4.
Question 6. Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Answer:
Given:
Two triangles, $\triangle ABC$ and $\triangle PQR$, such that $\triangle ABC \sim \triangle PQR$.
AD is the median of $\triangle ABC$ corresponding to side BC.
PM is the median of $\triangle PQR$ corresponding to side QR.
To Prove:
$\frac{\text{Area}(\triangle ABC)}{\text{Area}(\triangle PQR)} = \left(\frac{AD}{PM}\right)^2$.
Proof:
Since $\triangle ABC \sim \triangle PQR$, we know that:
1. The ratio of their areas is equal to the square of the ratio of their corresponding sides.
$\frac{\text{Area}(\triangle ABC)}{\text{Area}(\triangle PQR)} = \left(\frac{AB}{PQ}\right)^2 = \left(\frac{BC}{QR}\right)^2 = \left(\frac{AC}{PR}\right)^2$
... (i)
2. Their corresponding angles are equal.
$\angle A = \angle P, \angle B = \angle Q, \angle C = \angle R$
... (ii)
3. The ratio of their corresponding sides is equal.
$\frac{AB}{PQ} = \frac{BC}{QR} = \frac{AC}{PR}$
... (iii)
Since AD is the median to BC, D is the midpoint of BC. Thus, $BC = 2BD$.
Since PM is the median to QR, M is the midpoint of QR. Thus, $QR = 2QM$.
From equation (iii), we have:
$\frac{AB}{PQ} = \frac{BC}{QR}$
Substitute $BC = 2BD$ and $QR = 2QM$:
$\frac{AB}{PQ} = \frac{2BD}{2QM}$
$\frac{AB}{PQ} = \frac{BD}{QM}$
... (iv)
Now, consider the triangles $\triangle ABD$ and $\triangle PQM$.
From (ii), we have $\angle B = \angle Q$.
$\angle ABD = \angle PQM$
[Angle]
From (iv), we have the ratio of the sides including these angles:
$\frac{AB}{PQ} = \frac{BD}{QM}$
[Ratio of Sides]
Therefore, by the SAS similarity criterion:
$\triangle ABD \sim \triangle PQM$.
Since $\triangle ABD \sim \triangle PQM$, the ratio of their corresponding sides is equal.
$\frac{AB}{PQ} = \frac{BD}{QM} = \frac{AD}{PM}$
[Ratio of corresponding sides of similar triangles]
From this, we get:
$\frac{AB}{PQ} = \frac{AD}{PM}$
... (v)
Now, substitute the result from equation (v) into equation (i):
From (i): $\frac{\text{Area}(\triangle ABC)}{\text{Area}(\triangle PQR)} = \left(\frac{AB}{PQ}\right)^2$
Replacing $\frac{AB}{PQ}$ with $\frac{AD}{PM}$:
$\frac{\text{Area}(\triangle ABC)}{\text{Area}(\triangle PQR)} = \left(\frac{AD}{PM}\right)^2$
Thus, the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Hence Proved.
Question 7. Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
Answer:
Given:
A square ABCD.
An equilateral triangle described on one side of the square (let's say $\triangle BCE$ on side BC).
An equilateral triangle described on one of its diagonals (let's say $\triangle ACF$ on diagonal AC).
To Prove:
Area($\triangle BCE$) = $\frac{1}{2}$ Area($\triangle ACF$).
(Area of equilateral triangle on side = half the area of equilateral triangle on diagonal).
Proof:
Let the side length of the square ABCD be $a$.
So, $AB = BC = CD = DA = a$.
Consider the right-angled triangle $\triangle ABC$. By the Pythagorean theorem:
$AC^2 = AB^2 + BC^2$
$AC^2 = a^2 + a^2$
$AC^2 = 2a^2$
$AC = \sqrt{2a^2} = a\sqrt{2}$.
This is the length of the diagonal of the square.
Now, consider the equilateral triangle $\triangle BCE$ described on side BC.
The side length of $\triangle BCE$ is $BC = a$.
Consider the equilateral triangle $\triangle ACF$ described on diagonal AC.
The side length of $\triangle ACF$ is $AC = a\sqrt{2}$.
All equilateral triangles are similar to each other because all their angles are equal to $60^\circ$.
Therefore, $\triangle BCE \sim \triangle ACF$.
According to the theorem on the areas of similar triangles, the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
$\frac{\text{Area}(\triangle BCE)}{\text{Area}(\triangle ACF)} = \left(\frac{\text{Side of } \triangle BCE}{\text{Side of } \triangle ACF}\right)^2$
Substitute the side lengths:
$\frac{\text{Area}(\triangle BCE)}{\text{Area}(\triangle ACF)} = \left(\frac{BC}{AC}\right)^2$
$\frac{\text{Area}(\triangle BCE)}{\text{Area}(\triangle ACF)} = \left(\frac{a}{a\sqrt{2}}\right)^2$
Simplify the expression:
$\frac{\text{Area}(\triangle BCE)}{\text{Area}(\triangle ACF)} = \left(\frac{\cancel{a}}{\cancel{a}\sqrt{2}}\right)^2$
$\frac{\text{Area}(\triangle BCE)}{\text{Area}(\triangle ACF)} = \left(\frac{1}{\sqrt{2}}\right)^2$
$\frac{\text{Area}(\triangle BCE)}{\text{Area}(\triangle ACF)} = \frac{1^2}{(\sqrt{2})^2}$
$\frac{\text{Area}(\triangle BCE)}{\text{Area}(\triangle ACF)} = \frac{1}{2}$
Rearranging the equation:
Area($\triangle BCE$) = $\frac{1}{2}$ Area($\triangle ACF$).
This proves that the area of the equilateral triangle described on one side of the square is equal to half the area of the equilateral triangle described on one of its diagonals.
Hence Proved.
Tick the correct answer and justify :
Question 8. ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is
(A) 2 : 1
(B) 1 : 2
(C) 4 : 1
(D) 1 : 4
Answer:
Given:
$\triangle ABC$ and $\triangle BDE$ are two equilateral triangles.
D is the mid-point of BC.
To Find:
The ratio $\frac{\text{Area}(\triangle ABC)}{\text{Area}(\triangle BDE)}$.
Solution:
Since $\triangle ABC$ and $\triangle BDE$ are equilateral triangles, all their angles are $60^\circ$. Therefore, all equilateral triangles are similar to each other.
$\triangle ABC \sim \triangle BDE$.
Let the side length of $\triangle ABC$ be $s$. So, $AB = BC = AC = s$.
Since D is the mid-point of BC:
$BD = \frac{1}{2} BC = \frac{s}{2}$.
Since $\triangle BDE$ is an equilateral triangle, its side length is BD.
Side length of $\triangle BDE = BD = \frac{s}{2}$.
We know that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
$\frac{\text{Area}(\triangle ABC)}{\text{Area}(\triangle BDE)} = \left(\frac{\text{Side of } \triangle ABC}{\text{Side of } \triangle BDE}\right)^2$
Using corresponding sides BC and BD:
$\frac{\text{Area}(\triangle ABC)}{\text{Area}(\triangle BDE)} = \left(\frac{BC}{BD}\right)^2$
Substitute the side lengths in terms of $s$:
$\frac{\text{Area}(\triangle ABC)}{\text{Area}(\triangle BDE)} = \left(\frac{s}{s/2}\right)^2$
Simplify the expression:
$\frac{\text{Area}(\triangle ABC)}{\text{Area}(\triangle BDE)} = \left(s \times \frac{2}{s}\right)^2$
$\frac{\text{Area}(\triangle ABC)}{\text{Area}(\triangle BDE)} = (2)^2$
$\frac{\text{Area}(\triangle ABC)}{\text{Area}(\triangle BDE)} = 4$
The ratio can be written as $\frac{4}{1}$ or 4 : 1.
Conclusion:
The ratio of the areas of triangles ABC and BDE is 4 : 1.
Comparing with the options:
(A) 2 : 1
(B) 1 : 2
(C) 4 : 1
(D) 1 : 4
The correct option is (C) 4 : 1.
Question 9. Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
(A) 2 : 3
(B) 4 : 9
(C) 81 : 16
(D) 16 : 81
Answer:
Given:
Let the two similar triangles be denoted as Triangle 1 and Triangle 2.
The ratio of the corresponding sides of the two similar triangles is given as $4 : 9$.
To Find:
The ratio of the areas of these two triangles.
Solution:
We use the theorem which states that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Let the ratio of the sides be $s_1 : s_2$, where $s_1$ and $s_2$ are the lengths of corresponding sides of the two similar triangles.
Given, $\frac{s_1}{s_2} = \frac{4}{9}$.
Let Area($\triangle_1$) and Area($\triangle_2$) be the areas of the two similar triangles.
According to the theorem, the ratio of their areas is:
$\frac{\text{Area}(\triangle_1)}{\text{Area}(\triangle_2)} = \left(\frac{s_1}{s_2}\right)^2$
Substitute the given ratio of sides into the formula:
$\frac{\text{Area}(\triangle_1)}{\text{Area}(\triangle_2)} = \left(\frac{4}{9}\right)^2$
Now, calculate the square of the ratio:
$\left(\frac{4}{9}\right)^2 = \frac{4^2}{9^2} = \frac{16}{81}$
Thus, the ratio of the areas of the two similar triangles is $16 : 81$.
Comparing this ratio with the given options, we find that it matches option (D).
The final answer is:
(D) 16 : 81
Example 10 to 14 (Before Exercise 6.5)
Example 10. In Fig. 6.48, ∠ACB = 90° and CD⊥AB. Prove that $\frac{BC^{2}}{AC^{2}}$ = $\frac{BD}{AD}$ .

Answer:
Given:
In $\triangle$ACB, $\angle$ACB = $90^\circ$.
CD $\perp$ AB.
To Prove:
$\frac{BC^{2}}{AC^{2}}$ = $\frac{BD}{AD}$
Proof:
Consider the triangles $\triangle$ADC and $\triangle$ACB.
$\angle$ADC = $\angle$ACB = $90^\circ$
$\angle$CAD = $\angle$CAB
(Common angle)
Therefore, by AA similarity criterion,
$\triangle$ADC $\sim$ $\triangle$ACB
Since the triangles are similar, the ratio of corresponding sides is equal:
$\frac{AD}{AC} = \frac{CD}{CB} = \frac{AC}{AB}$
Taking the first and third ratios:
$\frac{AD}{AC} = \frac{AC}{AB}$
Cross-multiplying gives:
$AC^2 = AD \times AB$
Now, consider the triangles $\triangle$CDB and $\triangle$ACB.
$\angle$CDB = $\angle$ACB = $90^\circ$
$\angle$CBD = $\angle$CBA
(Common angle)
Therefore, by AA similarity criterion,
$\triangle$CDB $\sim$ $\triangle$ACB
Since the triangles are similar, the ratio of corresponding sides is equal:
$\frac{CD}{AC} = \frac{DB}{CB} = \frac{CB}{AB}$
Taking the second and third ratios:
$\frac{DB}{CB} = \frac{CB}{AB}$
Cross-multiplying gives:
$CB^2 = DB \times AB$
We need to prove $\frac{BC^2}{AC^2} = \frac{BD}{AD}$. Let's substitute the expressions for $BC^2$ and $AC^2$ we found:
$\frac{BC^2}{AC^2} = \frac{DB \times AB}{AD \times AB}$
Cancel the common term $AB$ from the numerator and denominator:
$\frac{BC^2}{AC^2} = \frac{DB}{AD}$
Rearranging the terms in the numerator and denominator of the right side gives the required result:
$\frac{BC^2}{AC^2} = \frac{BD}{AD}$
Hence Proved.
Example 11. A ladder is placed against a wall such that its foot is at a distance of 2.5 m from the wall and its top reaches a window 6 m above the ground. Find the length of the ladder.
Answer:
Given:
Distance of the foot of the ladder from the wall = $2.5$ m.
Height the top of the ladder reaches on the wall = $6$ m.
To Find:
The length of the ladder.
Solution:
Let the ladder be represented by the hypotenuse of a right-angled triangle. The wall is one leg and the ground is the other leg.
Let the length of the ladder be $l$.
Let the distance of the foot of the ladder from the wall be $b = 2.5$ m.
Let the height the top of the ladder reaches on the wall be $h = 6$ m.
According to the Pythagorean theorem, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
So, $l^2 = b^2 + h^2$
Substitute the given values:
$l^2 = (2.5)^2 + (6)^2$
Calculate the squares:
$(2.5)^2 = 2.5 \times 2.5 = 6.25$
$(6)^2 = 6 \times 6 = 36$
Substitute these values back into the equation:
$l^2 = 6.25 + 36$
$l^2 = 42.25$
To find the length $l$, take the square root of both sides:
$l = \sqrt{42.25}$
We need to find the square root of $42.25$.
$\sqrt{42.25} = \sqrt{\frac{4225}{100}} = \frac{\sqrt{4225}}{\sqrt{100}}$
$\sqrt{100} = 10$
To find $\sqrt{4225}$, we can use prime factorization or estimation.
Since the number ends in 5, its square root must end in 5. We can estimate the range. $60^2 = 3600$ and $70^2 = 4900$. So the square root is between 60 and 70 and ends in 5. The possible number is 65.
$65 \times 65 = 4225$
So, $\sqrt{4225} = 65$.
Therefore,
$l = \frac{65}{10}$
$l = 6.5$
The length of the ladder is $6.5$ m.
The final answer is:
The length of the ladder is $6.5$ m.
Example 12. In Fig. 6.50, if AD ⊥ BC, prove that AB2 + CD2 = BD2 + AC2 .
Answer:
Given:
In $\triangle$ABC, AD $\perp$ BC.
To Prove:
AB$^2$ + CD$^2$ = BD$^2$ + AC$^2$
Proof:
Since AD $\perp$ BC, $\triangle$ADB and $\triangle$ADC are right-angled triangles with the right angle at D.
In right-angled $\triangle$ADB, by the Pythagorean theorem, we have:
AB$^2$ = AD$^2$ + BD$^2$
Rearranging this equation to express AD$^2$:
AD$^2$ = AB$^2$ - BD$^2$
In right-angled $\triangle$ADC, by the Pythagorean theorem, we have:
AC$^2$ = AD$^2$ + CD$^2$
Rearranging this equation to express AD$^2$:
AD$^2$ = AC$^2$ - CD$^2$
Since both expressions are equal to AD$^2$, we can equate them:
AB$^2$ - BD$^2$ = AC$^2$ - CD$^2$
Now, rearrange the terms to get the desired result. Add BD$^2$ to both sides and add CD$^2$ to both sides:
AB$^2$ + CD$^2$ = AC$^2$ + BD$^2$
Rearranging the terms on the right side gives:
AB$^2$ + CD$^2$ = BD$^2$ + AC$^2$
Thus, the required relationship is proved.
Hence Proved.
Example 13. BL and CM are medians of a triangle ABC right angled at A. Prove that 4 (BL2 + CM2 ) = 5 BC2 .
Answer:
Given:
In $\triangle$ABC, $\angle$A = $90^\circ$.
BL and CM are medians of $\triangle$ABC.
To Prove:
$4 (BL^2 + CM^2 ) = 5 BC^2$
Proof:
Since BL is a median, L is the midpoint of AC.
So, $AL = LC = \frac{1}{2} AC$.
Since CM is a median, M is the midpoint of AB.
So, $AM = MB = \frac{1}{2} AB$.
In $\triangle$ABC, which is right-angled at A, by the Pythagorean theorem:
$BC^2 = AB^2 + AC^2$
Consider the right-angled triangle $\triangle$ABL (right-angled at A).
By the Pythagorean theorem:
$BL^2 = AB^2 + AL^2$
Substitute $AL = \frac{1}{2} AC$:
$BL^2 = AB^2 + \left(\frac{1}{2} AC\right)^2$
$BL^2 = AB^2 + \frac{1}{4} AC^2$
Multiply by 4:
$4 BL^2 = 4 AB^2 + AC^2$
Consider the right-angled triangle $\triangle$ACM (right-angled at A).
By the Pythagorean theorem:
$CM^2 = AC^2 + AM^2$
Substitute $AM = \frac{1}{2} AB$:
$CM^2 = AC^2 + \left(\frac{1}{2} AB\right)^2$
$CM^2 = AC^2 + \frac{1}{4} AB^2$
Multiply by 4:
$4 CM^2 = 4 AC^2 + AB^2$
Now, add the equations for $4 BL^2$ and $4 CM^2$:
$4 BL^2 + 4 CM^2 = (4 AB^2 + AC^2) + (4 AC^2 + AB^2)$
$4 (BL^2 + CM^2) = 4 AB^2 + AB^2 + AC^2 + 4 AC^2$
$4 (BL^2 + CM^2) = 5 AB^2 + 5 AC^2$
$4 (BL^2 + CM^2) = 5 (AB^2 + AC^2)$
From the first step, we know $AB^2 + AC^2 = BC^2$. Substitute this into the equation:
$4 (BL^2 + CM^2) = 5 BC^2$
Thus, the required relationship is proved.
Hence Proved.
Example 14. O is any point inside a rectangle ABCD (see Fig. 6.52). Prove that OB2 + OD2 = OA2 + OC2 .

Answer:
Given:
ABCD is a rectangle.
O is any point inside the rectangle.
To Prove:
$OB^2 + OD^2 = OA^2 + OC^2$
Construction:
Draw a line PQ through O parallel to AB and DC, where P is on AD and Q is on BC.
Since PQ is parallel to AB and DC, and ABCD is a rectangle (so AD $\parallel$ BC and $\angle$A = $90^\circ$), APQB and PQCD are rectangles. Thus, $\angle$APO = $\angle$BQP = $\angle$CQP = $\angle$DPO = $90^\circ$.
Proof:
Consider the right-angled triangle $\triangle$OAP.
By Pythagorean theorem:
$OA^2 = OP^2 + AP^2$
Consider the right-angled triangle $\triangle$OBQ.
By Pythagorean theorem:
$OB^2 = OQ^2 + BQ^2$
Since APQB is a rectangle, AP = BQ.
So, $OB^2 = OQ^2 + AP^2$
Consider the right-angled triangle $\triangle$OCQ.
By Pythagorean theorem:
$OC^2 = OQ^2 + CQ^2$
Consider the right-angled triangle $\triangle$ODP.
By Pythagorean theorem:
$OD^2 = OP^2 + DP^2$
Since PQCD is a rectangle, CQ = DP.
So, $OD^2 = OP^2 + CQ^2$
Now, let's add the expressions for $OB^2$ and $OD^2$:
$OB^2 + OD^2 = (OQ^2 + AP^2) + (OP^2 + CQ^2)$
$OB^2 + OD^2 = OQ^2 + AP^2 + OP^2 + CQ^2$
Next, let's add the expressions for $OA^2$ and $OC^2$:
$OA^2 + OC^2 = (OP^2 + AP^2) + (OQ^2 + CQ^2)$
$OA^2 + OC^2 = OP^2 + AP^2 + OQ^2 + CQ^2$
Comparing the results from adding $OB^2 + OD^2$ and $OA^2 + OC^2$, we see that the expressions are identical (just the terms are reordered).
$OB^2 + OD^2 = OQ^2 + AP^2 + OP^2 + CQ^2$
$OA^2 + OC^2 = OP^2 + AP^2 + OQ^2 + CQ^2$
Therefore,
$OB^2 + OD^2 = OA^2 + OC^2$
Thus, the required relationship is proved.
Hence Proved.
Exercise 6.5
Question 1. Sides of triangles are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse.
(i) 7 cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
(iii) 50 cm, 80 cm, 100 cm
(iv) 13 cm, 12 cm, 5 cm
Answer:
To determine if the given sides form a right triangle, we use the converse of the Pythagorean theorem. According to this theorem, if the square of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle, and the longest side is the hypotenuse.
(i) Sides are 7 cm, 24 cm, 25 cm.
The longest side is 25 cm.
Let $a = 7$ cm, $b = 24$ cm, and $c = 25$ cm.
Calculate the square of the longest side:
$c^2 = 25^2 = 625$
Calculate the sum of the squares of the other two sides:
$a^2 + b^2 = 7^2 + 24^2$
$a^2 + b^2 = 49 + 576$
$a^2 + b^2 = 625$
Compare $c^2$ and $a^2 + b^2$:
$c^2 = a^2 + b^2$ ($625 = 625$)
Since the square of the longest side is equal to the sum of the squares of the other two sides, the triangle is a right triangle.
The length of the hypotenuse is the longest side, which is 25 cm.
Conclusion: The sides 7 cm, 24 cm, and 25 cm form a right triangle. The hypotenuse is 25 cm.
(ii) Sides are 3 cm, 8 cm, 6 cm.
The longest side is 8 cm.
Let $a = 3$ cm, $b = 6$ cm, and $c = 8$ cm.
Calculate the square of the longest side:
$c^2 = 8^2 = 64$
Calculate the sum of the squares of the other two sides:
$a^2 + b^2 = 3^2 + 6^2$
$a^2 + b^2 = 9 + 36$
$a^2 + b^2 = 45$
Compare $c^2$ and $a^2 + b^2$:
$c^2 \neq a^2 + b^2$ ($64 \neq 45$)
Since the square of the longest side is not equal to the sum of the squares of the other two sides, the triangle is not a right triangle.
Conclusion: The sides 3 cm, 8 cm, and 6 cm do not form a right triangle.
(iii) Sides are 50 cm, 80 cm, 100 cm.
The longest side is 100 cm.
Let $a = 50$ cm, $b = 80$ cm, and $c = 100$ cm.
Calculate the square of the longest side:
$c^2 = 100^2 = 10000$
Calculate the sum of the squares of the other two sides:
$a^2 + b^2 = 50^2 + 80^2$
$a^2 + b^2 = 2500 + 6400$
$a^2 + b^2 = 8900$
Compare $c^2$ and $a^2 + b^2$:
$c^2 \neq a^2 + b^2$ ($10000 \neq 8900$)
Since the square of the longest side is not equal to the sum of the squares of the other two sides, the triangle is not a right triangle.
Conclusion: The sides 50 cm, 80 cm, and 100 cm do not form a right triangle.
(iv) Sides are 13 cm, 12 cm, 5 cm.
The longest side is 13 cm.
Let $a = 12$ cm, $b = 5$ cm, and $c = 13$ cm.
Calculate the square of the longest side:
$c^2 = 13^2 = 169$
Calculate the sum of the squares of the other two sides:
$a^2 + b^2 = 12^2 + 5^2$
$a^2 + b^2 = 144 + 25$
$a^2 + b^2 = 169$
Compare $c^2$ and $a^2 + b^2$:
$c^2 = a^2 + b^2$ ($169 = 169$)
Since the square of the longest side is equal to the sum of the squares of the other two sides, the triangle is a right triangle.
The length of the hypotenuse is the longest side, which is 13 cm.
Conclusion: The sides 13 cm, 12 cm, and 5 cm form a right triangle. The hypotenuse is 13 cm.
Question 2. PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM2 = QM . MR.
Answer:
Given:
In $\triangle$PQR, $\angle$P = $90^\circ$.
M is a point on QR such that PM $\perp$ QR.
To Prove:
$PM^2 = QM \cdot MR$
Proof:
In $\triangle$PQR, $\angle$P = $90^\circ$ and PM $\perp$ QR. This means that $\triangle$PQR, $\triangle$MPQ, and $\triangle$MRP are all similar to each other.
Consider $\triangle$MPQ and $\triangle$MRP.
$\angle$PMQ = $\angle$PMR
(Both are $90^\circ$ as PM $\perp$ QR)
In $\triangle$MPQ, $\angle$MPQ + $\angle$P QM + $\angle$PMQ = $180^\circ$ (Sum of angles in a triangle).
$\angle$MPQ + $\angle$P QM + $90^\circ$ = $180^\circ$
$\angle$MPQ = $90^\circ - \angle$P QM
In $\triangle$PQR, $\angle$QPR + $\angle$PQR + $\angle$PRQ = $180^\circ$ (Sum of angles in a triangle).
$90^\circ$ + $\angle$PQR + $\angle$PRQ = $180^\circ$
$\angle$PQR + $\angle$PRQ = $90^\circ$
$\angle$PRQ = $90^\circ - \angle$PQR
Since $\angle$PQR is the same as $\angle$P QM, we have $\angle$PRQ = $90^\circ - \angle$P QM.
Comparing the expressions for $\angle$MPQ and $\angle$PRQ:
$\angle$MPQ = $\angle$PRQ
(Both equal to $90^\circ - \angle$Q)
Similarly, we can show $\angle$PQM = $\angle$RPM.
Therefore, by AAA similarity criterion,
$\triangle$MPQ $\sim$ $\triangle$MRP
Since the triangles are similar, the ratio of their corresponding sides is equal.
Taking the ratio of corresponding sides opposite to equal angles:
$\frac{MP}{MR} = \frac{MQ}{MP} = \frac{PQ}{RP}$
From the first two ratios, we have:
$\frac{MP}{MR} = \frac{MQ}{MP}$
Cross-multiply:
$MP \times MP = MQ \times MR$
$MP^2 = MQ \times MR$
Since MP is the same as PM, we can write:
$PM^2 = QM \times MR$
Thus, the required relationship is proved.
Hence Proved.
Question 3. In Fig. 6.53, ABD is a triangle right angled at A and AC ⊥ BD. Show that

(i) AB2 = BC . BD
(ii) AC2 = BC . DC
(iii) AD2 = BD . CD
Answer:
Given:
In $\triangle$ABD, $\angle$BAD = $90^\circ$.
AC $\perp$ BD, with C on BD.
To Show:
(i) $AB^2 = BC \cdot BD$
(ii) $AC^2 = BC \cdot DC$
(iii) $AD^2 = BD \cdot CD$
Proof:
In $\triangle$ABD, since $\angle$BAD = $90^\circ$ and AC $\perp$ BD, AC is the altitude from the vertex of the right angle to the hypotenuse.
According to the theorem, if an altitude is drawn from the vertex of the right angle of a right triangle to the hypotenuse, then the triangles on either side of the altitude are similar to the whole triangle and also similar to each other.
Thus, we have:
$\triangle$ABC $\sim$ $\triangle$DBA
$\triangle$DAC $\sim$ $\triangle$DBA
$\triangle$ABC $\sim$ $\triangle$DAC
Also, since AC $\perp$ BD, $\angle$BCA = $90^\circ$ and $\angle$ACD = $90^\circ$.
In $\triangle$ABD, $\angle$B + $\angle$D = $90^\circ$ (Sum of angles in a triangle is $180^\circ$, $\angle$BAD = $90^\circ$).
In $\triangle$ABC (right-angled at C), $\angle$B + $\angle$BAC = $90^\circ$.
In $\triangle$ADC (right-angled at C), $\angle$D + $\angle$DAC = $90^\circ$.
From $\angle$B + $\angle$BAC = $90^\circ$ and $\angle$B + $\angle$D = $90^\circ$, we get $\angle$BAC = $\angle$D.
From $\angle$D + $\angle$DAC = $90^\circ$ and $\angle$B + $\angle$D = $90^\circ$, we get $\angle$DAC = $\angle$B.
(i) To show $AB^2 = BC \cdot BD$
Consider $\triangle$ABC and $\triangle$DBA.
$\angle$B = $\angle$B
(Common angle)
$\angle$BCA = $\angle$BAD
(Both are $90^\circ$)
By AA similarity criterion, $\triangle$ABC $\sim$ $\triangle$DBA.
The ratio of corresponding sides is equal:
$\frac{AB}{DB} = \frac{BC}{BA} = \frac{AC}{DA}$
Taking the first two ratios:
$\frac{AB}{DB} = \frac{BC}{AB}$
Cross-multiplying gives:
$AB \times AB = DB \times BC$
$AB^2 = BC \cdot BD$
This proves the first part.
(ii) To show $AC^2 = BC \cdot DC$
Consider $\triangle$ABC and $\triangle$DAC.
$\angle$B = $\angle$DAC
(Proved above)
$\angle$BCA = $\angle$ACD
(Both are $90^\circ$)
By AA similarity criterion, $\triangle$ABC $\sim$ $\triangle$DAC.
The ratio of corresponding sides is equal:
$\frac{AB}{DA} = \frac{BC}{AC} = \frac{AC}{DC}$
Taking the last two ratios:
$\frac{BC}{AC} = \frac{AC}{DC}$
Cross-multiplying gives:
$AC \times AC = BC \times DC$
$AC^2 = BC \cdot DC$
This proves the second part.
(iii) To show $AD^2 = BD \cdot CD$
Consider $\triangle$DAC and $\triangle$DBA.
$\angle$D = $\angle$D
(Common angle)
$\angle$ACD = $\angle$BAD
(Both are $90^\circ$)
By AA similarity criterion, $\triangle$DAC $\sim$ $\triangle$DBA.
The ratio of corresponding sides is equal:
$\frac{DA}{DB} = \frac{DC}{DA} = \frac{AC}{AB}$
Taking the first two ratios:
$\frac{DA}{DB} = \frac{DC}{DA}$
Cross-multiplying gives:
$DA \times DA = DB \times DC$
$AD^2 = BD \cdot CD$
This proves the third part.
Hence Shown.
Question 4. ABC is an isosceles triangle right angled at C. Prove that AB2 = 2AC2 .
Answer:
Given:
ABC is an isosceles triangle right angled at C.
This means $\angle$C = $90^\circ$ and AC = BC (since the angles opposite to equal sides are equal, and the acute angles in a right isosceles triangle are $45^\circ$, the sides opposite to them must be equal).
To Prove:
$AB^2 = 2AC^2$
Proof:
In $\triangle$ABC, since it is a right-angled triangle at C, we can apply the Pythagorean theorem.
According to the Pythagorean theorem, the square of the hypotenuse (AB) is equal to the sum of the squares of the other two sides (AC and BC).
$AB^2 = AC^2 + BC^2$
Since $\triangle$ABC is an isosceles triangle with the right angle at C, the sides containing the right angle must be equal.
Therefore, $AC = BC$.
Substitute $BC = AC$ into the Pythagorean equation:
$AB^2 = AC^2 + AC^2$
$AB^2 = 2AC^2$
Thus, the required relationship is proved.
Hence Proved.
Question 5. ABC is an isosceles triangle with AC = BC. If AB2 = 2AC2 , prove that ABC is a right triangle.
Answer:
Given:
ABC is an isosceles triangle with AC = BC.
$AB^2 = 2AC^2$.
To Prove:
ABC is a right triangle.
Proof:
We are given the equation:
$AB^2 = 2AC^2$
We can rewrite the right side of the equation as the sum of two terms:
$AB^2 = AC^2 + AC^2$
We are also given that $\triangle$ABC is an isosceles triangle with AC = BC.
We can substitute BC for AC in the equation above because AC = BC implies $AC^2 = BC^2$:
$AB^2 = AC^2 + BC^2$
This equation shows that the square of side AB is equal to the sum of the squares of sides AC and BC.
According to the converse of the Pythagorean theorem, if the square of one side of a triangle is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.
In the equation $AB^2 = AC^2 + BC^2$, the side AB is the longest side (as its square is equal to the sum of the squares of the other two sides).
The angle opposite to side AB is $\angle$C.
Therefore, by the converse of the Pythagorean theorem, the angle at C is a right angle.
$\angle$C = $90^\circ$
Since one of the angles ($\angle$C) of $\triangle$ABC is $90^\circ$, $\triangle$ABC is a right triangle.
Hence Proved.
Question 6. ABC is an equilateral triangle of side 2a. Find each of its altitudes.
Answer:
Given:
ABC is an equilateral triangle with side length $2a$.
This means $AB = BC = AC = 2a$.
To Find:
The length of each of its altitudes.
Solution:
Let AD be the altitude from vertex A to the side BC. Since ABC is an equilateral triangle, the altitude AD is also a median and an angle bisector.
Since AD is a median, D is the midpoint of BC.
Therefore, $BD = DC = \frac{1}{2} BC = \frac{1}{2} (2a) = a$.
In $\triangle$ADB, AD is perpendicular to BC, so $\angle$ADB = $90^\circ$.
Thus, $\triangle$ADB is a right-angled triangle with hypotenuse AB.
By the Pythagorean theorem in $\triangle$ADB:
$AB^2 = AD^2 + BD^2$
Substitute the known values: $AB = 2a$ and $BD = a$.
$(2a)^2 = AD^2 + a^2$
$4a^2 = AD^2 + a^2$
Subtract $a^2$ from both sides to find $AD^2$:
$AD^2 = 4a^2 - a^2$
$AD^2 = 3a^2$
Take the square root of both sides to find AD:
$AD = \sqrt{3a^2}$
$AD = \sqrt{3} \cdot \sqrt{a^2}$
$AD = a\sqrt{3}$
Since ABC is an equilateral triangle, all its altitudes are equal in length.
The length of each altitude is $a\sqrt{3}$.
The final answer is:
Each altitude of the equilateral triangle has a length of $a\sqrt{3}$.
Question 7. Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.
Answer:
Given:
ABCD is a rhombus.
Let the diagonals AC and BD intersect at point O.
To Prove:
The sum of the squares of the sides of the rhombus is equal to the sum of the squares of its diagonals.
That is, $AB^2 + BC^2 + CD^2 + DA^2 = AC^2 + BD^2$.
Proof:
We know that a rhombus is a quadrilateral where all four sides are equal in length. So, $AB = BC = CD = DA$.
We also know that the diagonals of a rhombus bisect each other at right angles.
Let the diagonals AC and BD intersect at O.
Then, $AO = OC = \frac{1}{2} AC$ and $BO = OD = \frac{1}{2} BD$.
Also, $\angle$AOB = $\angle$BOC = $\angle$COD = $\angle$DOA = $90^\circ$.
Consider the right-angled triangle $\triangle$AOB.
By the Pythagorean theorem, we have:
$AB^2 = AO^2 + BO^2$
Substitute the expressions for AO and BO in terms of the diagonals:
$AB^2 = \left(\frac{1}{2} AC\right)^2 + \left(\frac{1}{2} BD\right)^2$
$AB^2 = \frac{AC^2}{4} + \frac{BD^2}{4}$
$AB^2 = \frac{AC^2 + BD^2}{4}$
Multiply both sides by 4:
$4 AB^2 = AC^2 + BD^2$
Since all sides of the rhombus are equal, $AB = BC = CD = DA$, so $AB^2 = BC^2 = CD^2 = DA^2$.
The sum of the squares of the sides is $AB^2 + BC^2 + CD^2 + DA^2 = AB^2 + AB^2 + AB^2 + AB^2 = 4 AB^2$.
The sum of the squares of the diagonals is $AC^2 + BD^2$.
From the equation $4 AB^2 = AC^2 + BD^2$, we can see that the sum of the squares of the sides ($4 AB^2$) is equal to the sum of the squares of the diagonals ($AC^2 + BD^2$).
$AB^2 + BC^2 + CD^2 + DA^2 = AC^2 + BD^2$
This proves the required property of a rhombus.
Hence Proved.
Question 8. In Fig. 6.54, O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥AC and OF ⊥AB. Show that
(i) OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2 ,
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2 .
Answer:
Given:
O is a point in the interior of $\triangle$ABC.
OD $\perp$ BC, OE $\perp$ AC and OF $\perp$ AB.
To Show:
(i) $OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2 = AF^2 + BD^2 + CE^2$
(ii) $AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2$
Proof:
In $\triangle$OFA, since OF $\perp$ AB, $\angle$OFA = $90^\circ$. By Pythagorean theorem:
$OA^2 = OF^2 + AF^2$
Rearranging gives:
$AF^2 = OA^2 - OF^2$
In $\triangle$OFB, since OF $\perp$ AB, $\angle$OFB = $90^\circ$. By Pythagorean theorem:
$OB^2 = OF^2 + BF^2$
Rearranging gives:
$BF^2 = OB^2 - OF^2$
In $\triangle$ODB, since OD $\perp$ BC, $\angle$ODB = $90^\circ$. By Pythagorean theorem:
$OB^2 = OD^2 + BD^2$
Rearranging gives:
$BD^2 = OB^2 - OD^2$
In $\triangle$ODC, since OD $\perp$ BC, $\angle$ODC = $90^\circ$. By Pythagorean theorem:
$OC^2 = OD^2 + CD^2$
Rearranging gives:
$CD^2 = OC^2 - OD^2$
In $\triangle$OEC, since OE $\perp$ AC, $\angle$OEC = $90^\circ$. By Pythagorean theorem:
$OC^2 = OE^2 + CE^2$
Rearranging gives:
$CE^2 = OC^2 - OE^2$
In $\triangle$OEA, since OE $\perp$ AC, $\angle$OEA = $90^\circ$. By Pythagorean theorem:
$OA^2 = OE^2 + AE^2$
Rearranging gives:
$AE^2 = OA^2 - OE^2$
(i) To show $OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2 = AF^2 + BD^2 + CE^2$
Consider the left side of the equation:
$OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2$
Group the terms:
$(OA^2 - OF^2) + (OB^2 - OD^2) + (OC^2 - OE^2)$
Substitute the expressions for $AF^2$, $BD^2$, and $CE^2$ from the Pythagorean relations derived above:
$AF^2 = OA^2 - OF^2$
$BD^2 = OB^2 - OD^2$
$CE^2 = OC^2 - OE^2$
So, $OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2 = AF^2 + BD^2 + CE^2$.
This proves the first part.
(ii) To show $AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2$
From the Pythagorean relations derived above, we have:
$AF^2 = OA^2 - OF^2$
$BD^2 = OB^2 - OD^2$
$CE^2 = OC^2 - OE^2$
Summing the left sides:
$AF^2 + BD^2 + CE^2 = (OA^2 - OF^2) + (OB^2 - OD^2) + (OC^2 - OE^2)$
$AF^2 + BD^2 + CE^2 = OA^2 + OB^2 + OC^2 - OF^2 - OD^2 - OE^2$
Similarly, from the Pythagorean relations:
$AE^2 = OA^2 - OE^2$
$CD^2 = OC^2 - OD^2$
$BF^2 = OB^2 - OF^2$
Summing the left sides:
$AE^2 + CD^2 + BF^2 = (OA^2 - OE^2) + (OC^2 - OD^2) + (OB^2 - OF^2)$
$AE^2 + CD^2 + BF^2 = OA^2 + OC^2 + OB^2 - OE^2 - OD^2 - OF^2$
Rearranging the terms on the right side:
$AE^2 + CD^2 + BF^2 = OA^2 + OB^2 + OC^2 - OF^2 - OD^2 - OE^2$
Comparing the expressions for $AF^2 + BD^2 + CE^2$ and $AE^2 + CD^2 + BF^2$, we see that they are equal to the same expression ($OA^2 + OB^2 + OC^2 - OF^2 - OD^2 - OE^2$).
Therefore,
$AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2$
This proves the second part.
Hence Shown.
Question 9. A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.
Answer:
Given:
Length of the ladder = $10$ m.
Height the ladder reaches on the wall = $8$ m.
To Find:
The distance of the foot of the ladder from the base of the wall.
Solution:
Let the ladder, the wall, and the ground form a right-angled triangle, where the wall is perpendicular to the ground.
The ladder is the hypotenuse of this right-angled triangle.
The height the ladder reaches on the wall and the distance of the foot of the ladder from the base of the wall are the two legs of the right-angled triangle.
Let the length of the ladder be $l = 10$ m.
Let the height the ladder reaches on the wall be $h = 8$ m.
Let the distance of the foot of the ladder from the base of the wall be $d$ m.
According to the Pythagorean theorem, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
So, we have the relationship:
$l^2 = h^2 + d^2$
Substitute the given values into the equation:
$(10)^2 = (8)^2 + d^2$
Calculate the squares:
$100 = 64 + d^2$
To find the value of $d^2$, subtract 64 from both sides of the equation:
$d^2 = 100 - 64$
$d^2 = 36$
To find the distance $d$, take the square root of both sides of the equation. Since distance must be positive, we consider the positive square root:
$d = \sqrt{36}$
$d = 6$
The distance of the foot of the ladder from the base of the wall is $6$ metres.
The final answer is:
The distance of the foot of the ladder from the base of the wall is $6$ m.
Question 10. A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
Answer:
Given:
Height of the vertical pole = $18$ m.
Length of the guy wire attached to the pole = $24$ m.
The guy wire is taut, meaning it forms a straight line.
To Find:
The distance from the base of the pole where the stake should be driven.
Solution:
The vertical pole, the ground, and the taut guy wire form a right-angled triangle. The pole is perpendicular to the ground.
In this right-angled triangle:
The height of the pole is one leg.
The distance from the base of the pole to the stake is the other leg.
The length of the guy wire is the hypotenuse.
Let $h$ be the height of the pole ($h = 18$ m).
Let $w$ be the length of the guy wire ($w = 24$ m).
Let $d$ be the distance from the base of the pole to the stake.
According to the Pythagorean theorem, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
$w^2 = h^2 + d^2$
Substitute the given values into the equation:
$(24)^2 = (18)^2 + d^2$
Calculate the squares:
$24^2 = 24 \times 24 = 576$
$18^2 = 18 \times 18 = 324$
Substitute these values back into the equation:
$576 = 324 + d^2$
To find the value of $d^2$, subtract 324 from both sides of the equation:
$d^2 = 576 - 324$
$d^2 = 252$
To find the distance $d$, take the square root of both sides of the equation. Since distance must be positive, we consider the positive square root:
$d = \sqrt{252}$
To simplify the square root, we find the prime factorization of 252:
$\begin{array}{c|cc} 2 & 252 \\ \hline 2 & 126 \\ \hline 3 & 63 \\ \hline 3 & 21 \\ \hline 7 & 7 \\ \hline & 1 \end{array}$
So, $252 = 2 \times 2 \times 3 \times 3 \times 7 = 2^2 \times 3^2 \times 7$.
Now, substitute this into the square root expression:
$d = \sqrt{2^2 \times 3^2 \times 7}$
$d = \sqrt{2^2} \times \sqrt{3^2} \times \sqrt{7}$
$d = 2 \times 3 \times \sqrt{7}$
$d = 6\sqrt{7}$
The distance from the base of the pole to the stake should be $6\sqrt{7}$ metres so that the wire will be taut.
The final answer is:
The stake should be driven $6\sqrt{7}$ m away from the base of the pole.
Question 11. An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after $1\frac{1}{2}$ hours.
Answer:
Given:
Speed of the first aeroplane flying due north = $1000$ km/h.
Speed of the second aeroplane flying due west = $1200$ km/h.
Time duration = $1\frac{1}{2}$ hours = $\frac{3}{2}$ hours.
To Find:
The distance between the two planes after $1\frac{1}{2}$ hours.
Solution:
Let the airport be at point A. The first aeroplane flies due north and the second aeroplane flies due west from point A.
The path of the first aeroplane and the path of the second aeroplane are perpendicular to each other, forming a right angle at the airport (point A).
The distance covered by each aeroplane can be calculated using the formula: Distance = Speed $\times$ Time.
Distance covered by the first aeroplane (due north) in $\frac{3}{2}$ hours:
$d_{\text{North}} = \text{Speed}_{\text{North}} \times \text{Time}$
$d_{\text{North}} = 1000 \text{ km/h} \times \frac{3}{2} \text{ hours}$
$d_{\text{North}} = \frac{1000 \times 3}{2} \text{ km}$
$d_{\text{North}} = 500 \times 3 \text{ km}$
$d_{\text{North}} = 1500 \text{ km}$
Let the position of the first aeroplane after $\frac{3}{2}$ hours be point N.
So, $AN = 1500$ km.
Distance covered by the second aeroplane (due west) in $\frac{3}{2}$ hours:
$d_{\text{West}} = \text{Speed}_{\text{West}} \times \text{Time}$
$d_{\text{West}} = 1200 \text{ km/h} \times \frac{3}{2} \text{ hours}$
$d_{\text{West}} = \frac{1200 \times 3}{2} \text{ km}$
$d_{\text{West}} = 600 \times 3 \text{ km}$
$d_{\text{West}} = 1800 \text{ km}$
Let the position of the second aeroplane after $\frac{3}{2}$ hours be point W.
So, $AW = 1800$ km.
The airport A, the position of the first aeroplane N, and the position of the second aeroplane W form a right-angled triangle $\triangle$NAW, where the right angle is at A ($\angle$NAW = $90^\circ$).
The distance between the two planes after $\frac{3}{2}$ hours is the length of the hypotenuse NW.
By the Pythagorean theorem in $\triangle$NAW:
$NW^2 = AN^2 + AW^2$
Substitute the calculated distances:
$NW^2 = (1500)^2 + (1800)^2$
$NW^2 = 2250000 + 3240000$
$NW^2 = 5490000$
To find NW, take the square root of both sides:
$NW = \sqrt{5490000}$
$NW = \sqrt{549 \times 10000}$
$NW = \sqrt{549} \times \sqrt{10000}$
$NW = \sqrt{549} \times 100$
Now, let's find the prime factorization of 549 to simplify $\sqrt{549}$:
$\begin{array}{c|cc} 3 & 549 \\ \hline 3 & 183 \\ \hline 61 & 61 \\ \hline & 1 \end{array}$
So, $549 = 3 \times 3 \times 61 = 3^2 \times 61$.
$\sqrt{549} = \sqrt{3^2 \times 61} = \sqrt{3^2} \times \sqrt{61} = 3\sqrt{61}$
Substitute this back into the expression for NW:
$NW = 3\sqrt{61} \times 100$
$NW = 300\sqrt{61}$
The distance between the two planes after $1\frac{1}{2}$ hours is $300\sqrt{61}$ km.
The final answer is:
The two planes will be $300\sqrt{61}$ km apart after $1\frac{1}{2}$ hours.
Question 12. Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
Answer:
Given:
Height of the first pole = $6$ m.
Height of the second pole = $11$ m.
Distance between the feet of the poles = $12$ m.
To Find:
The distance between the tops of the poles.
Solution:
Let the two poles be represented by vertical lines AB and CD standing on a plane ground. Let A and C be the feet of the poles, and B and D be the tops of the poles, respectively.
Let the height of the first pole be $AB = 6$ m.
Let the height of the second pole be $CD = 11$ m.
The distance between the feet of the poles is $AC = 12$ m.
To find the distance between their tops (BD), we can construct a right-angled triangle.
Draw a line BE parallel to AC from point B to the pole CD. Point E lies on CD.
Since BE is parallel to AC and AB is parallel to CE (both are perpendicular to the ground AC), the quadrilateral ABEC is a rectangle.
Therefore, $AE = BC = 6$ m and $BE = AC = 12$ m.
Now, consider the segment ED. Since CD is the total height of the second pole and CE = AB, we have:
$ED = CD - CE$
$ED = 11 \text{ m} - 6 \text{ m}$
$ED = 5 \text{ m}$
Now, consider the triangle $\triangle$BED. Since BE is parallel to AC and AC is perpendicular to CD, BE is perpendicular to ED. Thus, $\triangle$BED is a right-angled triangle with the right angle at E ($\angle$BED = $90^\circ$).
The sides of the right-angled triangle $\triangle$BED are:
Base BE = $12$ m (distance between the feet)
Height ED = $5$ m (difference in heights)
Hypotenuse BD = distance between the tops (which we need to find)
By applying the Pythagorean theorem to $\triangle$BED:
$BD^2 = BE^2 + ED^2$
Substitute the values BE = 12 m and ED = 5 m:
$BD^2 = (12)^2 + (5)^2$
$BD^2 = 144 + 25$
$BD^2 = 169$
To find the distance BD, take the square root of both sides. Since distance must be positive, we take the positive square root:
$BD = \sqrt{169}$
$BD = 13$
The distance between the tops of the poles is $13$ m.
The final answer is:
The distance between the tops of the poles is $13$ m.
Question 13. D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2 + BD2 = AB2 + DE2
Answer:
Given:
In $\triangle$ABC, $\angle$C = $90^\circ$.
D is a point on side CA.
E is a point on side CB.
To Prove:
$AE^2 + BD^2 = AB^2 + DE^2$
Proof:
In $\triangle$ACE, which is right-angled at C, by the Pythagorean theorem, we have:
$AE^2 = AC^2 + CE^2$
In $\triangle$BCD, which is right-angled at C, by the Pythagorean theorem, we have:
$BD^2 = BC^2 + CD^2$
Add the equations for $AE^2$ and $BD^2$:
$AE^2 + BD^2 = (AC^2 + CE^2) + (BC^2 + CD^2)$
$AE^2 + BD^2 = AC^2 + CE^2 + BC^2 + CD^2$
In $\triangle$ABC, which is right-angled at C, by the Pythagorean theorem, we have:
$AB^2 = AC^2 + BC^2$
In $\triangle$DCE, which is right-angled at C, by the Pythagorean theorem, we have:
$DE^2 = CD^2 + CE^2$
Add the equations for $AB^2$ and $DE^2$:
$AB^2 + DE^2 = (AC^2 + BC^2) + (CD^2 + CE^2)$
$AB^2 + DE^2 = AC^2 + BC^2 + CD^2 + CE^2$
Comparing the expressions for $AE^2 + BD^2$ and $AB^2 + DE^2$, we see that they are equal:
$AC^2 + CE^2 + BC^2 + CD^2 = AC^2 + BC^2 + CD^2 + CE^2$
Therefore,
$AE^2 + BD^2 = AB^2 + DE^2$
Thus, the required relationship is proved.
Hence Proved.
Question 14. The perpendicular from A on side BC of a ∆ ABC intersects BC at D such that DB = 3 CD (see Fig. 6.55). Prove that 2 AB2 = 2 AC2 + BC2 .

Answer:
Given:
In $\triangle$ABC, AD $\perp$ BC, where D is a point on BC.
DB = 3 CD.
To Prove:
$2 AB^2 = 2 AC^2 + BC^2$
Proof:
Since AD $\perp$ BC, $\triangle$ADB and $\triangle$ADC are right-angled triangles with the right angle at D.
In right-angled $\triangle$ADB, by the Pythagorean theorem:
$AB^2 = AD^2 + DB^2$
In right-angled $\triangle$ADC, by the Pythagorean theorem:
$AC^2 = AD^2 + CD^2$
From this equation, we can express $AD^2$ as:
$AD^2 = AC^2 - CD^2$
Substitute the expression for $AD^2$ from the second equation into the first equation:
$AB^2 = (AC^2 - CD^2) + DB^2$
$AB^2 = AC^2 - CD^2 + DB^2$
We are given that DB = 3 CD.
The length of side BC is the sum of BD and CD (since D lies on BC):
$BC = BD + CD$
Substitute DB = 3 CD into this equation:
$BC = 3 CD + CD$
$BC = 4 CD$
From this, we can express CD in terms of BC:
$CD = \frac{BC}{4}$
Now, substitute this value of CD back into the equation DB = 3 CD:
$DB = 3 \left(\frac{BC}{4}\right)$
$DB = \frac{3 BC}{4}$
Now, substitute the expressions for CD and DB in terms of BC into the equation $AB^2 = AC^2 - CD^2 + DB^2$:
$AB^2 = AC^2 - \left(\frac{BC}{4}\right)^2 + \left(\frac{3 BC}{4}\right)^2$
$AB^2 = AC^2 - \frac{BC^2}{16} + \frac{9 BC^2}{16}$
Combine the terms with $BC^2$:
$AB^2 = AC^2 + \left(\frac{9 BC^2}{16} - \frac{BC^2}{16}\right)$
$AB^2 = AC^2 + \frac{9 BC^2 - BC^2}{16}$
$AB^2 = AC^2 + \frac{8 BC^2}{16}$
Simplify the fraction:
$AB^2 = AC^2 + \frac{1}{2} BC^2$
To eliminate the fraction, multiply the entire equation by 2:
$2 \times AB^2 = 2 \times \left(AC^2 + \frac{1}{2} BC^2\right)$
$2 AB^2 = 2 AC^2 + 2 \times \frac{1}{2} BC^2$
$2 AB^2 = 2 AC^2 + BC^2$
Thus, the required relationship is proved.
Hence Proved.
Question 15. In an equilateral triangle ABC, D is a point on side BC such that BD = $\frac{1}{3}$ BC. Prove that 9 AD2 = 7 AB2 .
Answer:
Given:
ABC is an equilateral triangle.
D is a point on side BC such that $BD = \frac{1}{3} BC$.
To Prove:
$9 AD^2 = 7 AB^2$
Construction:
Draw an altitude AE from A to BC, where E is on BC.
Proof:
Since $\triangle$ABC is an equilateral triangle, all its sides are equal. Let $AB = BC = AC = s$.
In an equilateral triangle, the altitude AE is also a median. Therefore, E is the midpoint of BC.
$BE = EC = \frac{1}{2} BC = \frac{1}{2} s$
We are given that $BD = \frac{1}{3} BC$. Substituting $BC = s$:
BD = $\frac{1}{3} s$
... (i)
Since E is the midpoint of BC, D lies between B and E (as $\frac{1}{3} < \frac{1}{2}$).
The distance DE can be found by subtracting BD from BE:
DE = BE - BD
... (ii)
Substitute the values of BE and BD:
$DE = \frac{1}{2} s - \frac{1}{3} s$
To subtract the fractions, find a common denominator (LCM of 2 and 3 is 6):
$DE = \frac{3}{6} s - \frac{2}{6} s$
$DE = \frac{3s - 2s}{6}$
DE = $\frac{1}{6} s$
... (iii)
In $\triangle$AEB, $\angle$AEB = $90^\circ$ (since AE is an altitude). By the Pythagorean theorem:
$AB^2 = AE^2 + BE^2$
Substitute $AB = s$ and $BE = \frac{1}{2} s$:
$s^2 = AE^2 + \left(\frac{1}{2} s\right)^2$
$s^2 = AE^2 + \frac{1}{4} s^2$
Rearranging the equation to find $AE^2$:
$AE^2 = s^2 - \frac{1}{4} s^2$
$AE^2 = \frac{4s^2 - s^2}{4}$
AE^2 = $\frac{3}{4} s^2$
... (iv)
Now, consider $\triangle$AED, which is right-angled at E ($\angle$AED = $90^\circ$). By the Pythagorean theorem:
$AD^2 = AE^2 + DE^2$
Substitute the expressions for $AE^2$ from (iv) and $DE$ from (iii):
$AD^2 = \frac{3}{4} s^2 + \left(\frac{1}{6} s\right)^2$
$AD^2 = \frac{3}{4} s^2 + \frac{1}{36} s^2$
To add the terms, find a common denominator (LCM of 4 and 36 is 36):
$AD^2 = \frac{3 s^2 \times 9}{4 \times 9} + \frac{1 s^2}{36}$
$AD^2 = \frac{27 s^2}{36} + \frac{s^2}{36}$
$AD^2 = \frac{27 s^2 + s^2}{36}$
$AD^2 = \frac{28 s^2}{36}$
Simplify the fraction by dividing the numerator and denominator by their greatest common divisor, which is 4:
$AD^2 = \frac{\cancel{28}^{7} s^2}{\cancel{36}_{9}}$
$AD^2 = \frac{7}{9} s^2$
Multiply both sides of the equation by 9:
$9 AD^2 = 9 \times \left(\frac{7}{9} s^2\right)$
$9 AD^2 = 7 s^2$
Since $s = AB$, we can substitute $s^2 = AB^2$:
$9 AD^2 = 7 AB^2$
Thus, the required relationship is proved.
Hence Proved.
Question 16. In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Answer:
Given:
ABC is an equilateral triangle.
To Prove:
Three times the square of one side is equal to four times the square of one of its altitudes.
Let $s$ be the side length of the equilateral triangle and $h$ be the length of its altitude. We need to prove $3s^2 = 4h^2$.
Construction:
Draw an altitude AD from vertex A to side BC, such that D lies on BC.
Proof:
In an equilateral triangle, the altitude from a vertex to the opposite side is also a median to that side.
Therefore, D is the midpoint of BC.
Since ABC is an equilateral triangle, all its sides are equal in length. Let $AB = BC = AC = s$.
As D is the midpoint of BC, we have $BD = DC = \frac{1}{2} BC = \frac{s}{2}$.
The altitude AD is perpendicular to BC, so $\angle$ADB = $90^\circ$.
Thus, $\triangle$ADB is a right-angled triangle with hypotenuse AB and legs AD and BD.
By applying the Pythagorean theorem in $\triangle$ADB, we have:
$AB^2 = AD^2 + BD^2$
Substitute the lengths in terms of $s$ and $h$: $AB = s$, $AD = h$, and $BD = \frac{s}{2}$.
$s^2 = h^2 + \left(\frac{s}{2}\right)^2$
Calculate the square of $\frac{s}{2}$:
$s^2 = h^2 + \frac{s^2}{4}$
Now, we want to rearrange this equation to relate $s^2$ and $h^2$. Subtract $\frac{s^2}{4}$ from both sides:
$s^2 - \frac{s^2}{4} = h^2$
Combine the terms on the left side by finding a common denominator:
$\frac{4s^2}{4} - \frac{s^2}{4} = h^2$
$\frac{4s^2 - s^2}{4} = h^2$
$\frac{3s^2}{4} = h^2$
Multiply both sides of the equation by 4 to clear the denominator:
$4 \times \frac{3s^2}{4} = 4 \times h^2$
$3s^2 = 4h^2$
This equation shows that three times the square of the side length ($s^2$) is equal to four times the square of the altitude length ($h^2$).
Therefore, three times the square of one side of an equilateral triangle is equal to four times the square of one of its altitudes.
Hence Proved.
Question 17. Tick the correct answer and justify : In ∆ABC, AB = 6$\sqrt{3}$ cm, AC = 12 cm and BC = 6 cm. The angle B is :
(A) 120°
(B) 60°
(C) 90°
(D) 45°
Answer:
Given:
In $\triangle$ABC, the side lengths are:
AB = $6\sqrt{3}$ cm
AC = $12$ cm
BC = $6$ cm
To Find:
The measure of angle B.
Solution and Justification:
We can use the converse of the Pythagorean theorem to determine if $\triangle$ABC is a right triangle.
First, identify the longest side. The lengths are approximately:
AB = $6\sqrt{3} \approx 6 \times 1.732 = 10.392$ cm
AC = $12$ cm
BC = $6$ cm
The longest side is AC = $12$ cm.
Now, calculate the square of the longest side:
$AC^2 = (12)^2 = 144$
Next, calculate the sum of the squares of the other two sides (AB and BC):
$AB^2 = (6\sqrt{3})^2 = 6^2 \times (\sqrt{3})^2 = 36 \times 3 = 108$
$BC^2 = (6)^2 = 36$
Sum of squares of other two sides = $AB^2 + BC^2 = 108 + 36 = 144$
Compare the square of the longest side with the sum of the squares of the other two sides:
$AC^2 = 144$
$AB^2 + BC^2 = 144$
Since $AC^2 = AB^2 + BC^2$, by the converse of the Pythagorean theorem, the triangle ABC is a right triangle.
In a right triangle, the angle opposite the hypotenuse (the longest side) is the right angle ($90^\circ$).
The longest side is AC, and the angle opposite to side AC is $\angle$B.
Therefore, $\angle$B = $90^\circ$.
This matches option (C).
The final answer is:
(C) 90°
Exercise 6.6 (Optional)
Question 1. In Fig. 6.56, PS is the bisector of ∠QPR of ∆ PQR. Prove that $\frac{QS}{SR}$ = $\frac{PQ}{PR}$ .
Answer:
Given:
In $\triangle$ PQR, PS is the angle bisector of $\angle$QPR, with point S on side QR.
To Prove:
$\frac{QS}{SR} = \frac{PQ}{PR}$.
Construction:
Draw a line through R parallel to PS, intersecting QP extended at point T.
Join RT.
Proof:
By construction, PS $\parallel$ RT.
Consider the transversal PT intersecting the parallel lines PS and RT.
$\angle$QPS = $\angle$PTR
(Corresponding angles)
Consider the transversal PR intersecting the parallel lines PS and RT.
$\angle$SPR = $\angle$PRT
(Alternate interior angles)
Given that PS is the angle bisector of $\angle$QPR:
$\angle$QPS = $\angle$SPR
(Given)
From the above relations ($\angle$QPS = $\angle$PTR, $\angle$SPR = $\angle$PRT, and $\angle$QPS = $\angle$SPR), we can conclude:
$\angle$PTR = $\angle$PRT
Now, consider $\triangle$ PRT. Since $\angle$PTR = $\angle$PRT, the sides opposite these equal angles are equal.
PT = PR
(Sides opposite equal angles are equal)
Next, consider $\triangle$ QRT.
We have PS $\parallel$ RT (by construction), and the line segment PS intersects the sides QT (which is QP extended) and QR at points P and S respectively.
By the Basic Proportionality Theorem (BPT), also known as Thales' Theorem, in $\triangle$ QRT, the line PS which is parallel to side RT divides the other two sides QT and QR proportionally.
Therefore, we have:
$\frac{QP}{PT} = \frac{QS}{SR}$
Now, substitute the equality PT = PR (which we proved from $\triangle$ PRT being isosceles) into this proportion:
$\frac{QP}{PR} = \frac{QS}{SR}$
Rearranging the terms to match the statement we need to prove:
$\frac{QS}{SR} = \frac{QP}{PR}$
Since QP is the same as PQ, we can write:
$\frac{QS}{SR} = \frac{PQ}{PR}$
Thus, the required relationship is proved.
Hence Proved.
Question 2. In Fig. 6.57, D is a point on hypotenuse AC of ∆ABC, such that BD ⊥AC, DM ⊥ BC and DN ⊥ AB. Prove that :
(i) DM2 = DN . MC
(ii) DN2 = DM . AN
Answer:
Given:
In $\triangle$ ABC, $\angle$ ABC = $90^\circ$.
D is a point on hypotenuse AC such that BD $\perp$ AC.
DM $\perp$ BC, with M on BC.
DN $\perp$ AB, with N on AB.
To Prove:
(i) $DM^2 = DN \cdot MC$
(ii) $DN^2 = DM \cdot AN$
Proof:
Since DN $\perp$ AB and DM $\perp$ BC, and $\angle$ ABC = $90^\circ$, the quadrilateral BNDM has $\angle$ NBM = $90^\circ$, $\angle$ BND = $90^\circ$ (since DN $\perp$ AB), and $\angle$ BMD = $90^\circ$ (since DM $\perp$ BC).
A quadrilateral with three right angles is a rectangle. Therefore, BNDM is a rectangle.
In a rectangle, opposite sides are equal. So, $DN = BM$ and $DM = BN$.
In $\triangle$ ABC, BD is the altitude from the right angle B to the hypotenuse AC. According to the properties of a right triangle with an altitude to the hypotenuse, we have the following angle equalities:
$\angle$ ABD = $\angle$ BCA
(Let's call it $\angle$ C)
$\angle$ CBD = $\angle$ BAC
(Let's call it $\angle$ A)
Also, in right $\triangle$ ABC, $\angle$ A + $\angle$ C = $90^\circ$.
(i) To prove $DM^2 = DN \cdot MC$
Consider the right-angled triangles $\triangle$ BMD and $\triangle$ DMC (both are right-angled at M).
$\angle$ BMD = $\angle$ DMC
(Each is $90^\circ$ as DM $\perp$ BC)
In $\triangle$ BMD, $\angle$ MBD = $\angle$ CBD = $\angle$ A.
The third angle in $\triangle$ BMD is $\angle$ BDM = $180^\circ - 90^\circ - \angle$ A = $90^\circ - \angle$ A. Since $\angle$ A + $\angle$ C = $90^\circ$, we have $90^\circ - \angle$ A = $\angle$ C.
$\angle$ BDM = $\angle$ C
In $\triangle$ DMC, $\angle$ DCM = $\angle$ C.
The third angle in $\triangle$ DMC is $\angle$ CDM = $180^\circ - 90^\circ - \angle$ C = $90^\circ - \angle$ C. Since $\angle$ A + $\angle$ C = $90^\circ$, we have $90^\circ - \angle$ C = $\angle$ A.
$\angle$ CDM = $\angle$ A
Now, compare the angles of $\triangle$ BMD and $\triangle$ DMC:
$\angle$ MBD = $\angle$ CDM
(Both equal to $\angle$ A)
$\angle$ BDM = $\angle$ DCM
(Both equal to $\angle$ C)
$\angle$ BMD = $\angle$ DMC
(Both equal to $90^\circ$)
By AAA similarity criterion, $\triangle$ BMD $\sim$ $\triangle$ DMC.
Since the triangles are similar, the ratio of their corresponding sides is equal. Matching the sides opposite equal angles:
$\frac{BM}{DM}$ (Opposite $\angle$ BDM = $\angle$ C and $\angle$ DCM = $\angle$ C)
$\frac{MD}{MC}$ (Opposite $\angle$ MBD = $\angle$ A and $\angle$ CDM = $\angle$ A)
$\frac{BD}{DC}$ (Opposite $\angle$ BMD = $90^\circ$ and $\angle$ DMC = $90^\circ$)
So, we have $\frac{BM}{DM} = \frac{MD}{MC} = \frac{BD}{DC}$.
Taking the first two ratios:
$\frac{BM}{DM} = \frac{DM}{MC}$
Cross-multiplying gives:
$DM^2 = BM \cdot MC$
From the rectangle BNDM, we know that $BM = DN$.
Substitute $BM = DN$ into the equation:
$DM^2 = DN \cdot MC$
This proves the first part.
(ii) To prove $DN^2 = DM \cdot AN$
Consider the right-angled triangles $\triangle$ ADN and $\triangle$ DNB (both are right-angled at N).
$\angle$ AND = $\angle$ DNB
(Each is $90^\circ$ as DN $\perp$ AB)
In $\triangle$ ADN, $\angle$ DAN = $\angle$ A.
The third angle in $\triangle$ ADN is $\angle$ ADN = $180^\circ - 90^\circ - \angle$ A = $90^\circ - \angle$ A = $\angle$ C.
$\angle$ ADN = $\angle$ C
In $\triangle$ DNB, $\angle$ DBN = $\angle$ ABD = $\angle$ C.
The third angle in $\triangle$ DNB is $\angle$ NDB = $180^\circ - 90^\circ - \angle$ C = $90^\circ - \angle$ C = $\angle$ A.
$\angle$ NDB = $\angle$ A
Now, compare the angles of $\triangle$ ADN and $\triangle$ DNB:
$\angle$ DAN = $\angle$ NDB
(Both equal to $\angle$ A)
$\angle$ ADN = $\angle$ DBN
(Both equal to $\angle$ C)
$\angle$ AND = $\angle$ DNB
(Both equal to $90^\circ$)
By AAA similarity criterion, $\triangle$ ADN $\sim$ $\triangle$ DNB.
Since the triangles are similar, the ratio of their corresponding sides is equal. Matching the sides opposite equal angles:
$\frac{AD}{DB}$ (Opposite $\angle$ AND = $90^\circ$ and $\angle$ DNB = $90^\circ$)
$\frac{DN}{NB}$ (Opposite $\angle$ DAN = $\angle$ A and $\angle$ NDB = $\angle$ A)
$\frac{AN}{DN}$ (Opposite $\angle$ ADN = $\angle$ C and $\angle$ DBN = $\angle$ C)
So, we have $\frac{AD}{DB} = \frac{DN}{NB} = \frac{AN}{DN}$.
Taking the last two ratios:
$\frac{DN}{NB} = \frac{AN}{DN}$
Cross-multiplying gives:
$DN^2 = AN \cdot NB$
From the rectangle BNDM, we know that $NB = DM$.
Substitute $NB = DM$ into the equation:
$DN^2 = AN \cdot DM$
Rearranging the terms on the right side:
$DN^2 = DM \cdot AN$
This proves the second part.
Hence Proved.
Question 3. In Fig. 6.58, ABC is a triangle in which ∠ABC > 90° and AD ⊥ CB produced. Prove that AC2 = AB2 + BC2 + 2 BC . BD.
Answer:
Given:
In $\triangle$ ABC, $\angle$ ABC > $90^\circ$.
AD $\perp$ CB produced, with D on CB produced.
To Prove:
$AC^2 = AB^2 + BC^2 + 2 BC \cdot BD$.
Proof:
Since AD $\perp$ CB produced, $\triangle$ ADB and $\triangle$ ADC are right-angled triangles with the right angle at D.
Consider the right-angled triangle $\triangle$ ADB.
By the Pythagorean theorem, the square of the hypotenuse AB is equal to the sum of the squares of the other two sides AD and DB.
AB$^2$ = AD$^2$ + DB$^2$
(Pythagorean theorem in $\triangle$ ADB)
Rearranging this equation to express AD$^2$:
AD$^2$ = AB$^2$ - DB$^2$
... (1)
Now, consider the right-angled triangle $\triangle$ ADC.
By the Pythagorean theorem, the square of the hypotenuse AC is equal to the sum of the squares of the other two sides AD and DC.
AC$^2$ = AD$^2$ + DC$^2$
(Pythagorean theorem in $\triangle$ ADC)
From the figure, since D lies on CB produced, the length DC is the sum of DB and BC.
DC = DB + BC
Substitute this expression for DC into the equation for $AC^2$:
$AC^2 = AD^2 + (DB + BC)^2$
Expand the term $(DB + BC)^2$:
$(DB + BC)^2 = DB^2 + BC^2 + 2 \cdot DB \cdot BC$
Substitute this back into the equation for $AC^2$:
$AC^2 = AD^2 + DB^2 + BC^2 + 2 DB \cdot BC$
We can group the terms $AD^2$ and $DB^2$:
$AC^2 = (AD^2 + DB^2) + BC^2 + 2 DB \cdot BC$
From equation (1), we know that $AD^2 + DB^2 = AB^2$. Substitute this into the equation:
$AC^2 = AB^2 + BC^2 + 2 DB \cdot BC$
Rearranging the last term to match the required form:
$AC^2 = AB^2 + BC^2 + 2 BC \cdot BD$
Thus, the required relationship is proved.
Hence Proved.
Question 4. In Fig. 6.59, ABC is a triangle in which ∠ ABC < 90° and AD ⊥ BC. Prove that AC2 = AB2 + BC2 – 2 BC . BD.
Answer:
Given:
In $\triangle$ ABC, $\angle$ ABC < $90^\circ$.
AD $\perp$ BC, with D on BC.
To Prove:
$AC^2 = AB^2 + BC^2 – 2 BC \cdot BD$.
Proof:
Since AD $\perp$ BC, $\triangle$ ADB and $\triangle$ ADC are right-angled triangles with the right angle at D.
Consider the right-angled triangle $\triangle$ ADB.
By the Pythagorean theorem, the square of the hypotenuse AB is equal to the sum of the squares of the other two sides AD and BD.
AB$^2$ = AD$^2$ + BD$^2$
(Pythagorean theorem in $\triangle$ ADB)
Rearranging this equation to express AD$^2$:
AD$^2$ = AB$^2$ - BD$^2$
... (1)
Now, consider the right-angled triangle $\triangle$ ADC.
By the Pythagorean theorem, the square of the hypotenuse AC is equal to the sum of the squares of the other two sides AD and DC.
AC$^2$ = AD$^2$ + DC$^2$
(Pythagorean theorem in $\triangle$ ADC)
From the figure, since D lies on the line segment BC, the length BC is the sum of BD and DC, or the difference depending on the position of D. As $\angle$ ABC < $90^\circ$ and AD $\perp$ BC, point D must lie between B and C if $\angle$ACB is acute, or on the extension of BC if $\angle$ACB is obtuse. The diagram shows D is on BC itself, so $BC = BD + DC$. Thus, $DC = BC - BD$.
DC = BC - BD
Substitute this expression for DC into the equation for $AC^2$:
$AC^2 = AD^2 + (BC - BD)^2$
Expand the term $(BC - BD)^2$:
$(BC - BD)^2 = BC^2 + BD^2 - 2 \cdot BC \cdot BD$
Substitute this back into the equation for $AC^2$:
$AC^2 = AD^2 + BC^2 + BD^2 - 2 BC \cdot BD$
We can group the terms $AD^2$ and $BD^2$:
$AC^2 = (AD^2 + BD^2) + BC^2 - 2 BC \cdot BD$
From equation (1), we know that $AD^2 + BD^2 = AB^2$. Substitute this into the equation:
$AC^2 = AB^2 + BC^2 - 2 BC \cdot BD$
Thus, the required relationship is proved.
Hence Proved.
Question 5. In Fig. 6.60, AD is a median of a triangle ABC and AM ⊥ BC. Prove that :
(i) AC2 = AD2 + BC . DM + $\left( \frac{BC}{2}\right)^{2}$
(ii) AB2 = AD2 – BC . DM + $\left( \frac{BC}{2}\right)^{2}$
(iii) AC2 + AB2 = 2 AD2 + $\frac{1}{2}$ BC2
Answer:
Given:
In $\triangle$ ABC, AD is a median, so D is the midpoint of BC.
AM $\perp$ BC, so $\angle$ AMC = $\angle$ AMB = $90^\circ$, where M is on the line containing BC.
The figure shows M lying on the line segment BC, and specifically between B and D.
To Prove:
(i) $AC^2 = AD^2 + BC \cdot DM + \left( \frac{BC}{2}\right)^{2}$
(ii) $AB^2 = AD^2 – BC \cdot DM + \left( \frac{BC}{2}\right)^{2}$
(iii) $AC^2 + AB^2 = 2 AD^2 + \frac{1}{2} BC^2$
Proof:
Since AM $\perp$ BC, $\triangle$ AMC, $\triangle$ AMB, and $\triangle$ AMD are right-angled triangles at M.
In right-angled $\triangle$ AMC, by the Pythagorean theorem:
AC$^2$ = AM$^2$ + MC$^2$
(Pythagorean theorem)
... (1)
In right-angled $\triangle$ AMB, by the Pythagorean theorem:
AB$^2$ = AM$^2$ + BM$^2$
(Pythagorean theorem)
... (2)
In right-angled $\triangle$ AMD, by the Pythagorean theorem:
AD$^2$ = AM$^2$ + DM$^2$
(Pythagorean theorem)
Rearranging this equation to express $AM^2$:
AM$^2$ = AD$^2$ - DM$^2$
... (3)
Substitute the expression for $AM^2$ from (3) into equation (1):
$AC^2 = (AD^2 - DM^2) + MC^2$
$AC^2 = AD^2 - DM^2 + MC^2$
Substitute the expression for $AM^2$ from (3) into equation (2):
$AB^2 = (AD^2 - DM^2) + BM^2$
$AB^2 = AD^2 - DM^2 + BM^2$
Since AD is a median, D is the midpoint of BC.
BD = DC = $\frac{1}{2}$ BC
(D is midpoint of BC)
From the figure, M lies on BC, and is between B and D. This implies the order of points on the line is B, M, D, C.
In this configuration, the lengths of the segments BM and MC can be expressed in terms of BD, DC, and DM:
BM = BD - DM
(M is between B and D)
BM = $\frac{BC}{2}$ - DM
... (4)
MC = MD + DC
(D is between M and C)
MC = DM + $\frac{BC}{2}$
... (5)
Square equation (4):
$BM^2 = \left(\frac{BC}{2} - DM\right)^2$
$BM^2 = \left(\frac{BC}{2}\right)^2 - 2 \cdot \frac{BC}{2} \cdot DM + DM^2$
BM$^2$ = $\left(\frac{BC}{2}\right)^2 - BC \cdot DM + DM^2$
... (6)
Square equation (5):
$MC^2 = \left(DM + \frac{BC}{2}\right)^2$
$MC^2 = DM^2 + 2 \cdot DM \cdot \frac{BC}{2} + \left(\frac{BC}{2}\right)^2$
MC$^2$ = DM$^2$ + BC $\cdot$ DM + $\left(\frac{BC}{2}\right)^2$
... (7)
(i) To prove $AC^2 = AD^2 + BC \cdot DM + \left( \frac{BC}{2}\right)^{2}$
Substitute the expression for $MC^2$ from (7) into the equation $AC^2 = AD^2 - DM^2 + MC^2$:
$AC^2 = AD^2 - DM^2 + \left[DM^2 + BC \cdot DM + \left(\frac{BC}{2}\right)^2\right]$
$AC^2 = AD^2 - DM^2 + DM^2 + BC \cdot DM + \left(\frac{BC}{2}\right)^2$
$AC^2 = AD^2 + BC \cdot DM + \left(\frac{BC}{2}\right)^2$
This proves the first part.
(ii) To prove $AB^2 = AD^2 – BC \cdot DM + \left( \frac{BC}{2}\right)^{2}$
Substitute the expression for $BM^2$ from (6) into the equation $AB^2 = AD^2 - DM^2 + BM^2$:
$AB^2 = AD^2 - DM^2 + \left[\left(\frac{BC}{2}\right)^2 - BC \cdot DM + DM^2\right]$
$AB^2 = AD^2 - DM^2 + \left(\frac{BC}{2}\right)^2 - BC \cdot DM + DM^2$
$AB^2 = AD^2 + \left(\frac{BC}{2}\right)^2 - BC \cdot DM$
$AB^2 = AD^2 – BC \cdot DM + \left( \frac{BC}{2}\right)^{2}$
This proves the second part.
(iii) To prove $AC^2 + AB^2 = 2 AD^2 + \frac{1}{2} BC^2$
Add the results from part (i) and part (ii):
$AC^2 + AB^2 = \left(AD^2 + BC \cdot DM + \left(\frac{BC}{2}\right)^2\right) + \left(AD^2 - BC \cdot DM + \left(\frac{BC}{2}\right)^2\right)$
Group like terms:
$AC^2 + AB^2 = (AD^2 + AD^2) + (BC \cdot DM - BC \cdot DM) + \left(\left(\frac{BC}{2}\right)^2 + \left(\frac{BC}{2}\right)^2\right)$
$AC^2 + AB^2 = 2 AD^2 + 0 + \left(\frac{BC^2}{4} + \frac{BC^2}{4}\right)$
$AC^2 + AB^2 = 2 AD^2 + \frac{2 BC^2}{4}$
$AC^2 + AB^2 = 2 AD^2 + \frac{1}{2} BC^2$
This proves the third part (Apollonius's Theorem for median AD).
Hence Proved.
Question 6. Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.
Answer:
Given:
ABCD is a parallelogram.
AC and BD are its diagonals.
To Prove:
The sum of the squares of the diagonals of the parallelogram is equal to the sum of the squares of its sides.
That is, $AC^2 + BD^2 = AB^2 + BC^2 + CD^2 + DA^2$.
Proof:
Let the parallelogram be ABCD.
In a parallelogram, opposite sides are equal in length. Thus, $AB = CD$ and $BC = DA$.
Also, in a parallelogram, consecutive angles are supplementary. Thus, $\angle ABC + \angle BCD = 180^\circ$ and $\angle BCD + \angle CDA = 180^\circ$, etc.
Consider $\triangle$ ABC. By the Law of Cosines in $\triangle$ ABC, we have:
AC$^2$ = AB$^2$ + BC$^2$ - 2(AB)(BC) $\cos(\angle ABC)$
(Law of Cosines in $\triangle$ ABC) ... (1)
Consider $\triangle$ BCD. By the Law of Cosines in $\triangle$ BCD, we have:
BD$^2$ = BC$^2$ + CD$^2$ - 2(BC)(CD) $\cos(\angle BCD)$
(Law of Cosines in $\triangle$ BCD) ... (2)
Since ABCD is a parallelogram, we know that $CD = AB$ and $\angle BCD = 180^\circ - \angle ABC$.
Using the trigonometric identity $\cos(180^\circ - \theta) = -\cos(\theta)$, we have $\cos(\angle BCD) = \cos(180^\circ - \angle ABC) = -\cos(\angle ABC)$.
Substitute $CD = AB$ and $\cos(\angle BCD) = -\cos(\angle ABC)$ into equation (2):
BD$^2$ = BC$^2$ + AB$^2$ - 2(BC)(AB) $(-\cos(\angle ABC))$
... (3)
BD$^2$ = BC$^2$ + AB$^2$ + 2(BC)(AB) $\cos(\angle ABC)$
Now, add equation (1) and equation (3):
AC$^2$ + BD$^2$ = (AB$^2$ + BC$^2$ - 2(AB)(BC) $\cos(\angle ABC)$) + (BC$^2$ + AB$^2$ + 2(BC)(AB) $\cos(\angle ABC)$)
Group the terms on the right side:
AC$^2$ + BD$^2$ = AB$^2$ + AB$^2$ + BC$^2$ + BC$^2$ - 2(AB)(BC) $\cos(\angle ABC)$ + 2(BC)(AB) $\cos(\angle ABC)$
The terms involving the cosine cancel each other out:
AC$^2$ + BD$^2$ = 2 AB$^2$ + 2 BC$^2$
Now, let's consider the sum of the squares of the sides of the parallelogram:
Sum of squares of sides = $AB^2 + BC^2 + CD^2 + DA^2$
Since $CD = AB$ and $DA = BC$ in a parallelogram, substitute these equalities:
Sum of squares of sides = $AB^2 + BC^2 + AB^2 + BC^2$
Sum of squares of sides = $2 AB^2 + 2 BC^2$
Comparing the expression for the sum of the squares of the diagonals ($AC^2 + BD^2$) and the expression for the sum of the squares of the sides ($2 AB^2 + 2 BC^2$), we see that they are equal.
Therefore, $AC^2 + BD^2 = AB^2 + BC^2 + CD^2 + DA^2$.
Thus, the sum of the squares of the diagonals of a parallelogram is equal to the sum of the squares of its sides.
Hence Proved.
Question 7. In Fig. 6.61, two chords AB and CD intersect each other at the point P. Prove that :
(i) ∆APC ~ ∆ DPB
(ii) AP . PB = CP . DP
Answer:
Given:
Two chords AB and CD intersect each other at point P inside a circle.
To Prove:
(i) $\triangle$APC $\sim$ $\triangle$ DPB
(ii) AP $\cdot$ PB = CP $\cdot$ DP
Proof:
(i) To prove $\triangle$APC $\sim$ $\triangle$ DPB
Consider the triangles $\triangle$APC and $\triangle$ DPB.
In $\triangle$APC and $\triangle$ DPB:
$\angle$APC = $\angle$DPB
(Vertically opposite angles are equal)
$\angle$CAP = $\angle$CDB
(Angles in the same segment subtended by arc CB are equal)
Therefore, by AA similarity criterion,
$\triangle$APC $\sim$ $\triangle$ DPB
This proves the first part.
(ii) To prove AP $\cdot$ PB = CP $\cdot$ DP
Since $\triangle$APC $\sim$ $\triangle$ DPB (proved in part i), the ratio of their corresponding sides is equal.
The corresponding sides are opposite to the equal angles:
- Side opposite $\angle$ACP is AP, and side opposite $\angle$DBP is DP. So, $\frac{AP}{DP}$.
- Side opposite $\angle$CAP is CP, and side opposite $\angle$CDB is BP (or PB). So, $\frac{CP}{PB}$.
- Side opposite $\angle$APC is AC, and side opposite $\angle$DPB is DB. So, $\frac{AC}{DB}$.
Thus, we have the proportionality:
$\frac{AP}{DP} = \frac{CP}{PB} = \frac{AC}{DB}$
Take the first two ratios:
$\frac{AP}{DP} = \frac{CP}{PB}$
Cross-multiply the terms:
$AP \times PB = DP \times CP$
Rearranging the terms on the right side gives:
$AP \cdot PB = CP \cdot DP$
This proves the second part.
Hence Proved.
Question 8. In Fig. 6.62, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ∆ PAC ~ ∆ PDB
(ii) PA . PB = PC . PD

Answer:
Given:
Two chords AB and CD of a circle, when produced, intersect each other at point P outside the circle.
To Prove:
(i) $\triangle$ PAC $\sim$ $\triangle$ PDB
(ii) PA $\cdot$ PB = PC $\cdot$ PD
Proof:
Consider the triangles $\triangle$ PAC and $\triangle$ PDB.
In $\triangle$ PAC and $\triangle$ PDB:
$\angle$APC = $\angle$DPB
(Common angle at P)
The points A, B, C, D lie on the circle, so ACBD forms a cyclic quadrilateral.
Consider the angles subtended by the arc BC at the circumference.
$\angle$BAC = $\angle$BDC
(Angles in the same segment subtended by arc BC are equal)
The angle $\angle$BAC in $\triangle$ PAC is the same as $\angle$PAC.
The angle $\angle$BDC in $\triangle$ PDB is the same as $\angle$PDB.
Therefore,
$\angle$PAC = $\angle$PDB
Now, we have two pairs of equal angles in $\triangle$ PAC and $\triangle$ PDB:
$\angle$P = $\angle$P
(Common)
$\angle$PAC = $\angle$PDB
(Angles subtended by arc BC)
Therefore, by AA similarity criterion,
$\triangle$ PAC $\sim$ $\triangle$ PDB
This proves the first part.
(i) $\triangle$ PAC $\sim$ $\triangle$ PDB is proved.
(ii) To prove PA $\cdot$ PB = PC $\cdot$ PD
Since $\triangle$ PAC $\sim$ $\triangle$ PDB (proved in part i), the ratio of their corresponding sides is equal.
Matching the corresponding vertices from the similarity statement $\triangle$ PAC $\sim$ $\triangle$ PDB:
- P corresponds to P (common angle).
- A corresponds to D (opposite to $\angle$PCA and $\angle$PBD - angles subtended by arc AD). No, A corresponds to D because $\angle$PAC = $\angle$PDB.
- C corresponds to B (opposite to $\angle$PAC and $\angle$PDB - angles subtended by arc AD). No, C corresponds to B because $\angle$PCA = $\angle$PBD.
Let's match angles correctly:
- Angle P in $\triangle$ PAC corresponds to angle P in $\triangle$ PDB.
- Angle PAC in $\triangle$ PAC corresponds to angle PDB in $\triangle$ PDB (since $\angle$PAC = $\angle$PDB).
- Angle PCA in $\triangle$ PAC corresponds to angle PBD in $\triangle$ PDB (the third angle).
So, the correspondence of vertices is P $\leftrightarrow$ P, A $\leftrightarrow$ D, C $\leftrightarrow$ B.
The ratio of corresponding sides is:
$\frac{PA}{PD} = \frac{AC}{DB} = \frac{PC}{PB}$
Taking the first and third ratios from the proportionality:
$\frac{PA}{PD} = \frac{PC}{PB}$
Cross-multiply the terms:
$PA \times PB = PD \times PC$
Rearranging the terms on the right side:
$PA \cdot PB = PC \cdot PD$
This proves the second part.
(ii) PA $\cdot$ PB = PC $\cdot$ PD is proved.
Question 9. In Fig. 6.63, D is a point on side BC of ∆ ABC such that $\frac{BD}{CD}$ = $\frac{AB}{AC}$ Prove that AD is the bisector of ∠ BAC.

Answer:
Given:
In $\triangle$ ABC, D is a point on side BC such that $\frac{BD}{CD} = \frac{AB}{AC}$.
To Prove:
AD is the bisector of $\angle$ BAC.
That is, to prove $\angle$ BAD = $\angle$ CAD.
Construction:
Extend segment BA to a point E such that AE = AC.
Join CE.
Proof:
Consider $\triangle$ ACE.
AE = AC
(By construction)
Therefore, $\triangle$ ACE is an isosceles triangle.
In an isosceles triangle, the angles opposite the equal sides are equal.
$\angle$ AEC = $\angle$ ACE
... (1)
We are given that $\frac{BD}{CD} = \frac{AB}{AC}$.
Since AE = AC (by construction), we can substitute AE for AC in the given ratio:
$\frac{BD}{CD} = \frac{AB}{AE}$
... (2)
Rearranging equation (2), we get:
$\frac{BD}{AB} = \frac{CD}{AE}$
Consider $\triangle$ BCE. We have the points A on BE and D on BC such that $\frac{BD}{CD} = \frac{AB}{AE}$.
This is the converse form of the Basic Proportionality Theorem (BPT) for $\triangle$ BCE, with transversal line AD cutting sides BE and BC.
However, the given ratio is $\frac{BD}{CD} = \frac{AB}{AC}$, and we substituted AC with AE, so $\frac{BD}{CD} = \frac{AB}{AE}$.
Let's rethink the construction and application of BPT.
Alternative Construction/Proof Approach:
Draw a line through C parallel to AD, intersecting BA extended at E.
Proof:
By construction, AD $\parallel$ EC.
Consider transversal BE intersecting parallel lines AD and EC.
$\angle$ BAD = $\angle$ AEC
(Corresponding angles)
... (3)
Consider transversal AC intersecting parallel lines AD and EC.
$\angle$ DAC = $\angle$ ACE
(Alternate interior angles)
... (4)
In $\triangle$ BCE, AD is parallel to EC and intersects sides BE and BC at A and D respectively.
By the Basic Proportionality Theorem (BPT):
$\frac{BD}{DC} = \frac{BA}{AE}$
We are given $\frac{BD}{CD} = \frac{AB}{AC}$. Note that $DC = CD$ and $BA = AB$.
So, we have $\frac{BD}{CD} = \frac{AB}{AC}$ and from BPT, $\frac{BD}{CD} = \frac{AB}{AE}$.
Comparing these two equations:
$\frac{AB}{AC} = \frac{AB}{AE}$
Since $AB \neq 0$, we can cancel AB from both sides:
$\frac{1}{AC} = \frac{1}{AE}$
This implies:
AC = AE
... (5)
Now, consider $\triangle$ ACE. Since AC = AE (from 5), $\triangle$ ACE is an isosceles triangle.
In an isosceles triangle, the angles opposite the equal sides are equal.
$\angle$ AEC = $\angle$ ACE
... (6)
From equations (3), (4), and (6):
We have $\angle$ BAD = $\angle$ AEC (3)
We have $\angle$ DAC = $\angle$ ACE (4)
We have $\angle$ AEC = $\angle$ ACE (6)
Therefore, from (3), (4), and (6), we can conclude that:
$\angle$ BAD = $\angle$ DAC
Since AD divides $\angle$ BAC into two equal angles, $\angle$ BAD and $\angle$ DAC, AD is the angle bisector of $\angle$ BAC.
Hence Proved.
Question 10. Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, how much string does she have out (see Fig. 6.64)? If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?
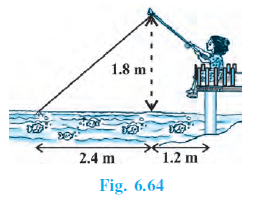
Answer:
Given:
Height of the tip of the fishing rod above the water = $1.8$ m.
Horizontal distance of the fly from the point directly under the tip of the rod = $2.4$ m.
Rate at which string is pulled in = $5$ cm per second.
Time duration for pulling in string = $12$ seconds.
To Find:
1. The initial length of the string out.
2. The horizontal distance of the fly from Nazima after 12 seconds (assuming Nazima is located at the point directly under the tip of the rod).
Solution:
We can model the situation as a right-angled triangle, where the vertical height from the rod tip to the water surface is one leg, the horizontal distance from the point under the tip to the fly on the water is the other leg, and the taut string is the hypotenuse.
Part 1: Calculate the initial length of the string.
Let the height of the rod tip above the water be $H = 1.8$ m.
Let the initial horizontal distance of the fly from the point under the tip be $D = 2.4$ m.
Let the initial length of the string be $L$.
Applying the Pythagorean theorem:
L$^2$ = H$^2$ + D$^2$
(Pythagorean theorem)
Substitute the given values:
L$^2$ = $(1.8)^2 + (2.4)^2$
Calculate the squares:
$(1.8)^2 = 1.8 \times 1.8 = 3.24$
$(2.4)^2 = 2.4 \times 2.4 = 5.76$
Substitute the squared values back into the equation:
L$^2$ = $3.24 + 5.76$
L$^2$ = $9.00$
To find L, take the square root of both sides:
$L = \sqrt{9}$
$L = 3$
The initial length of the string out is $3$ m.
Part 2: Calculate the horizontal distance after pulling in string.
Rate at which string is pulled in = $5$ cm/s.
Convert the rate to metres per second: $5$ cm = $\frac{5}{100}$ m = $0.05$ m.
Rate = $0.05$ m/s.
Time = $12$ seconds.
Amount of string pulled in = Rate $\times$ Time
Amount pulled in = $0.05$ m/s $\times$ $12$ s
Amount pulled in = $0.6$ m.
The initial length of the string was $3$ m.
New length of the string ($L'$) = Initial length - Amount pulled in
$L' = 3$ m - $0.6$ m
$L' = 2.4$ m.
The height of the rod tip above the water remains $H = 1.8$ m.
Let the new horizontal distance of the fly from the point under the tip be $D'$.
Applying the Pythagorean theorem to the new right triangle:
$(L')^2 = H^2 + (D')^2$
(Pythagorean theorem)
Substitute the new string length and the height:
$(2.4)^2 = (1.8)^2 + (D')^2$
We already calculated the squares:
$(2.4)^2 = 5.76$
$(1.8)^2 = 3.24$
Substitute these values:
$5.76 = 3.24 + (D')^2$
Rearrange the equation to find $(D')^2$:
$(D')^2 = 5.76 - 3.24$
$(D')^2 = 2.52$
To find $D'$, take the square root of both sides:
$D' = \sqrt{2.52}$
To simplify $\sqrt{2.52}$, find the prime factorization of 252:
$\begin{array}{c|cc} 2 & 252 \\ \hline 2 & 126 \\ \hline 3 & 63 \\ \hline 3 & 21 \\ \hline 7 & 7 \\ \hline & 1 \end{array}$
So, $252 = 2^2 \times 3^2 \times 7$.
Also, $2.52 = \frac{252}{100}$.
$D' = \sqrt{\frac{252}{100}} = \frac{\sqrt{252}}{\sqrt{100}} = \frac{\sqrt{2^2 \times 3^2 \times 7}}{10} = \frac{\sqrt{2^2} \times \sqrt{3^2} \times \sqrt{7}}{10} = \frac{2 \times 3 \times \sqrt{7}}{10}$
$D' = \frac{6\sqrt{7}}{10}$
Cancel the common factor 2 in the numerator and denominator:
$D' = \frac{\cancel{6}^{3}\sqrt{7}}{\cancel{10}_{5}}$
$D' = \frac{3\sqrt{7}}{5}$
The horizontal distance of the fly from the point directly under the tip of the rod after 12 seconds is $\frac{3\sqrt{7}}{5}$ m.
Assuming Nazima is located at the point directly under the tip of the rod, this is the horizontal distance of the fly from her.
The final answer is:
The initial string out is $3$ m.
The horizontal distance of the fly from her after 12 seconds is $\frac{3\sqrt{7}}{5}$ m.

